题目内容
(文)已知等比数列{xn}的公比是不为1的正数,数列{yn}满足yn•logxna=2(a>0,a≠1),当y4=15,y7=9时,数列{yn}的前k项和最大,则k的值为 ( )
| A.9 | B.10 | C.11 | D.12(yn=23-2n) |
依题意,yn=2logaxn,由yn-yn-1=2log(
)=2q (q为等比数列{xn}的公比)
∴数列{yn}是等差数列,又∵y4=15,y7=9
∴yn=23-2n,由yn≥0,得n≤11,即y11>0,y12<0
∴数列{yn}的前11项和最大
故选C
| xn |
| xn-1 |
∴数列{yn}是等差数列,又∵y4=15,y7=9
∴yn=23-2n,由yn≥0,得n≤11,即y11>0,y12<0
∴数列{yn}的前11项和最大
故选C

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,定义数列
,定义数列 为数列
为数列 =2,
=2,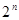 ,则数列
,则数列 =
=  ,
, ,则
,则 =
=