题目内容
已知函数f(x)=|x-a|x+b,给出下列命题:
①当a=0时,f(x)的图象关于点(0,b)成中心对称;
②当x>a时,f(x)是递增函数;
③f(x)=0至多有两个实数根;
④当0≤x≤a时,f(x)的最大值为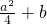 .
.
其中正确的序号是________.
①②④
分析:根据函数的单调性和奇偶性,对各个选项加以判断.利用奇函数图象关于原点对称,可得①正确;利用二次函数图象及其单调性,得出②正确;举出一个反例,可得③不正确;利用二次函数图象与性质,求函数的最值可得出④正确.
解答:对各个选项分别加以判别:
对于①,当a=0时,f(x)=|x|x+b,可得f(-x)=-|x|x+b
∴f(x)+f(-x)=2b,可得f(x)的图象关于点(0,b)成中心对称;
对于②,当x>a时,f(x)=x(x-a)+b,图象的对称轴为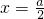 ,开口向上
,开口向上
因此在对称轴的右侧为增函数,所以当x>a时,f(x)是递增函数;
对于③,可以取a=3,b=-2时,f(x)=0有三个实数根:
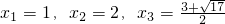 ,故③不正确;
,故③不正确;
对于④,当0≤x≤a时,f(x)=-x2+ax+b
当x= 时,函数的最大值为f(
时,函数的最大值为f( )=
)=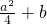 .
.
故答案为:①②④
点评:本题以函数的奇偶性和单调性为载体,考查了命题真假的判断,属于中档题,熟练掌握函数的基本性质是解决本题的关键所在.
分析:根据函数的单调性和奇偶性,对各个选项加以判断.利用奇函数图象关于原点对称,可得①正确;利用二次函数图象及其单调性,得出②正确;举出一个反例,可得③不正确;利用二次函数图象与性质,求函数的最值可得出④正确.
解答:对各个选项分别加以判别:
对于①,当a=0时,f(x)=|x|x+b,可得f(-x)=-|x|x+b
∴f(x)+f(-x)=2b,可得f(x)的图象关于点(0,b)成中心对称;
对于②,当x>a时,f(x)=x(x-a)+b,图象的对称轴为
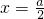 ,开口向上
,开口向上因此在对称轴的右侧为增函数,所以当x>a时,f(x)是递增函数;
对于③,可以取a=3,b=-2时,f(x)=0有三个实数根:
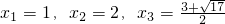 ,故③不正确;
,故③不正确;对于④,当0≤x≤a时,f(x)=-x2+ax+b
当x=
 时,函数的最大值为f(
时,函数的最大值为f( )=
)=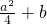 .
.故答案为:①②④
点评:本题以函数的奇偶性和单调性为载体,考查了命题真假的判断,属于中档题,熟练掌握函数的基本性质是解决本题的关键所在.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|