题目内容
 (2009•河北区二模)已知如图(1),梯形ABCD中,AD∥BC,∠ABC=∠BAD=
(2009•河北区二模)已知如图(1),梯形ABCD中,AD∥BC,∠ABC=∠BAD=| π | 2 |
(Ⅰ)求证:平面ABE⊥平面ABCD;
(Ⅱ)若以B、C、D、F为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(Ⅲ)当f(x)取得最大值时,求异面直线CD和BE所成角的余弦值.
分析:(1)由面面垂直的判定定理推出即可;
(2)过D作DH∥AE,则DG=AE,且DH⊥平面EBCF,由f(x)=VD-BFC =
×S△BFC×DH 求出f(x)的解析式,由二次函数的性质求出其最大值;
(3)作平行线得到∠AMN即为异面直线CD和BE所成的角,求出此角所在三角形的三边长,余弦定理求得θ的余弦值.
(2)过D作DH∥AE,则DG=AE,且DH⊥平面EBCF,由f(x)=VD-BFC =
| 1 |
| 3 |
(3)作平行线得到∠AMN即为异面直线CD和BE所成的角,求出此角所在三角形的三边长,余弦定理求得θ的余弦值.
解答:解:(Ⅰ)∵平面AEFD⊥平面EBCF,AE⊥EF,∴AE⊥平面EBCF,
∴AE⊥BC
∵BE⊥BC,
∴BC⊥平面ABE.
又BC?平面ABCD,
∴平面ABE⊥平面ABCD. …(4分)
(Ⅱ)∵AD∥平面BFC,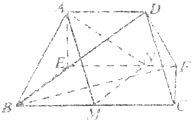
∴f(x)=VD-BFC=VA-BFC=
S△BFC•AE…6分
=
×
×4(4-x)x=-
(x-2)2+
≤
即x=2时,f(x)有最大值
. …(8分)
(Ⅲ)取BC中点M,作MN∥BE交EF于N,连结AM,AN,
∵MC∥AD,且MC=AD,
∴AMCD为平行四边形.∴AM∥CD
∴∠AMN即为异面直线CD和BE所成的角.…(10分)
计算得AN=2
,MN=2,AM=2
,
∴cos∠AMN=
…(12分)
∴AE⊥BC
∵BE⊥BC,
∴BC⊥平面ABE.
又BC?平面ABCD,
∴平面ABE⊥平面ABCD. …(4分)
(Ⅱ)∵AD∥平面BFC,

∴f(x)=VD-BFC=VA-BFC=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
即x=2时,f(x)有最大值
| 8 |
| 3 |
(Ⅲ)取BC中点M,作MN∥BE交EF于N,连结AM,AN,
∵MC∥AD,且MC=AD,
∴AMCD为平行四边形.∴AM∥CD
∴∠AMN即为异面直线CD和BE所成的角.…(10分)
计算得AN=2
| 2 |
| 3 |
∴cos∠AMN=
| ||
| 3 |
点评:本题考查求三棱锥的体积,求函数的最大值,求异面直线所成的角的余弦值,找出异面直线所成的角,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目