题目内容
已知圆C的圆心C在y轴上,且圆C与直线y=x+1相切,点A(-1,-2)在圆内,圆半径等于2
(1)求圆的方程;
(2)求经过点A的最短弦所在的直线l的方程.
| 2 |
(1)求圆的方程;
(2)求经过点A的最短弦所在的直线l的方程.
分析:(1)由题意设圆的标准方程为x2+(y-b)2=8,根据圆C与直线y=x+1相切,利用点到直线的距离公式建立关于b的等式,解出b=5或-3.由点A(-1,-2)在圆内加以检验,可得b=-3,所以圆的方程是x2+(y+3)2=8;
(2)根据圆的性质,可得当经过点A的弦最短时,直线l与AC所在直线垂直,由此算出直线l的斜率,利用直线方程的点斜式列式,化简即可得到所求直线l的方程.
(2)根据圆的性质,可得当经过点A的弦最短时,直线l与AC所在直线垂直,由此算出直线l的斜率,利用直线方程的点斜式列式,化简即可得到所求直线l的方程.
解答:解:(1)根据题意,圆心的坐标为C(0,b),半径r=2
,
设圆的标准方程为x2+(y-b)2=8,
∵圆C与直线y=x+1相切,
∴C(0,b)到直线y=x+1的距离等于半径,即
=2
,解之得b=5或-3.
∵点A(-1,-2)在圆内,
∴|CA|=
<2
,解之得-
-2<b<
-2.
因此,b=5不符合题意,可得b=-3.
∴圆的方程是x2+(y+3)2=8;
(2)当经过点A的弦最短时,其所在直线l与直线AC互相垂直,
∵AC的斜率k=
=-1,∴直线l的斜率k'=
=1,
可得直线l方程为y+2=x+1,即x-y-1=0.
| 2 |
设圆的标准方程为x2+(y-b)2=8,
∵圆C与直线y=x+1相切,
∴C(0,b)到直线y=x+1的距离等于半径,即
| |-b+1| | ||
|
| 2 |
∵点A(-1,-2)在圆内,
∴|CA|=
| (-1-0)2+(-2-b)2 |
| 2 |
| 7 |
| 7 |
因此,b=5不符合题意,可得b=-3.
∴圆的方程是x2+(y+3)2=8;
(2)当经过点A的弦最短时,其所在直线l与直线AC互相垂直,
∵AC的斜率k=
| -3+2 |
| 0+1 |
| -1 |
| k |
可得直线l方程为y+2=x+1,即x-y-1=0.
点评:本题给出圆满足的条件,求圆的方程并求经过圆内点A截得最短弦长的直线方程.着重考查了圆的标准方程、直线的基本量与基本形式和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
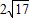 .
.