题目内容
已知圆C的圆心C在x轴的正半轴上,半径为5,圆C被直线x-y+3=0截得的弦长为2| 17 |
(1)求圆C的方程;
(2)设直线ax-y+5=0与圆相交于A,B两点,求实数a的取值范围;
(3)在(2)的条件下,是否存在实数a,使得A,B关于过点P(-2,4)的直线l对称?若存在,求出实数a的值;若不存在,请说明理由.
分析:(1)设⊙C的方程为(x-m)2+y2=25(m>0),由弦长公式求出m,即得圆C的方程.
(2) 由圆心到直线的距离等于半径,求得实数a的取值范围.
(3)设存在实数a,使得A,B关于l对称,则有
,解出实数a的值,得出结论.
(2) 由圆心到直线的距离等于半径,求得实数a的取值范围.
(3)设存在实数a,使得A,B关于l对称,则有
|
解答:解:(1)设⊙C的方程为(x-m)2+y2=25(m>0),由题意设
,
解得 m=1.故⊙C的方程为(x-1)2+y2=25.
(2)由题设知
<5,故12a2-5a>0,所以,a<0,或a>
.
故实数a的取值范围为(-∞,0)∪(
,+∞).
(3)设存在实数a,使得A,B关于l对称.∴PC⊥AB,又 a<0,或a>
,
即
,∴a=
,
∴存在实数a=
,满足题设.
|
解得 m=1.故⊙C的方程为(x-1)2+y2=25.
(2)由题设知
| |a+5| | ||
|
| 5 |
| 12 |
故实数a的取值范围为(-∞,0)∪(
| 5 |
| 12 |
(3)设存在实数a,使得A,B关于l对称.∴PC⊥AB,又 a<0,或a>
| 5 |
| 12 |
即
|
| 3 |
| 4 |
∴存在实数a=
| 3 |
| 4 |
点评:本题考查圆的标准方程以及直线和圆相交的性质,两直线垂直的性质,由存在实数a,使得A,B关于l对称得到
是解题的关键和难点.
|

练习册系列答案
相关题目
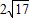 .
.