Question

5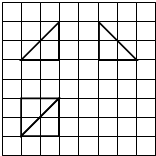．如图所示，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱与底面所成角的正弦值为$\frac{\sqrt{3}}{3}$．

Answer 1

分析 结合题意及图形，可知几何体为一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥，还原几何体，求解即可．

解答 解：由三视图可知，
此多面体是一个底面边长为2的正方形，
且有一条长为2的侧棱垂直于底面的四棱锥，
所以最长棱长为：$\sqrt{{2}^{2}+{2}^{2}+{2}^{2}}$=2$\sqrt{3}$．
这个多面体最长的一条棱与底面所成角的正弦值为：$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$．
故答案为：$\frac{\sqrt{3}}{3}$．

点评 本题考查了三视图视角下多面体棱长的最值问题，考查直线与平面所成角的求法．考查了同学们的识图能力以及由三视图还原物体的能力．