题目内容
(本题满分12分)
设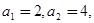 数列
数列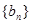 满足:
满足:
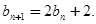
求数列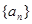 的通项公式.
的通项公式.
设
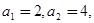 数列
数列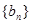 满足:
满足:
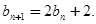
求数列
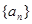 的通项公式.
的通项公式. 
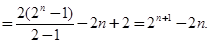
本试题主要是考查了递推关系式的运用。利用已知中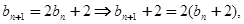 得到
得到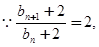 分析得到通项公式,然后利用分组求和法得到结论。
分析得到通项公式,然后利用分组求和法得到结论。
解析: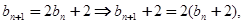
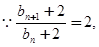
又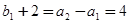 ,
,
 数列
数列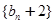 是首项为4,公比为2的等比数列.
是首项为4,公比为2的等比数列.
 .
. 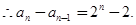
令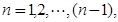 叠加得
叠加得 ,
,
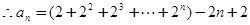
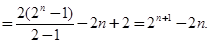
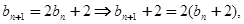 得到
得到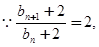 分析得到通项公式,然后利用分组求和法得到结论。
分析得到通项公式,然后利用分组求和法得到结论。解析:
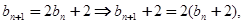
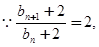
又
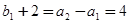 ,
,  数列
数列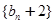 是首项为4,公比为2的等比数列.
是首项为4,公比为2的等比数列.  .
. 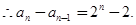
令
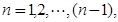 叠加得
叠加得 ,
, 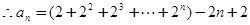
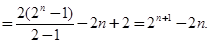

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
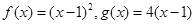 ,数列
,数列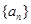 满足
满足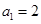 ,且
,且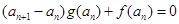 .
.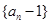 是否是等比数列?(5分)
是否是等比数列?(5分)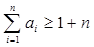 .(5分)
.(5分)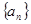 中,
中,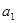 和
和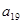 为方程
为方程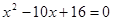 的两根,则
的两根,则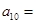 ( )
( )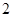

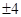
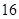
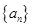 中,
中,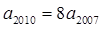 ,则公比
,则公比 的值为 ( )
的值为 ( )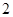
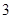

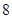
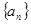 中, 若
中, 若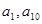 是方程
是方程 的两根,则
的两根,则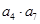 = .
= .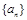 中,
中,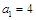 ,公比为q,前n项和为
,公比为q,前n项和为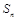 ,若数列
,若数列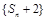 也是等比数列,则q等于
也是等比数列,则q等于 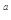 =3,2
=3,2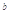 =6,2
=6,2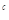 =12,则数列a,b,c是( )
=12,则数列a,b,c是( )
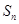 为等比数列
为等比数列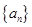 的前
的前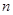 项和,已知
项和,已知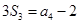 ,
,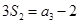 ,则公比
,则公比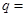 ( )
( )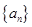 中,
中,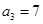 ,前3项之和
,前3项之和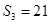 ,则公比
,则公比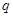 的值为 ( )
的值为 ( )
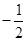
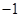 或
或