题目内容
19.点P为x轴上的一点,A(1,1),B(3,4),则|PA|+|PB|的最小值是$\sqrt{29}$.分析 先求出点A关于x轴对称的点A′的坐标,再用两点间的距离公式求出A′B的长即可.
解答 解:∵A点坐标为(1,1),
∴点A关于x轴对称的点A′(1,-1).
∵B点坐标为(3,4),
∴|A′B|=$\sqrt{(3-1)^{2}+(4+1)^{2}}$=$\sqrt{29}$.
∴|PA|+|PB|的最小值为$\sqrt{29}$.
故答案为:$\sqrt{29}$.
点评 本题考查的是轴对称-最短路线问题,熟知两点之间,线段最短是解答此题的关键

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
14.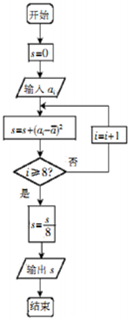 如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
 如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| 39 | 40 | 42 | 42 | 43 | 45 | 46 | 47 |
| A. | A | B. | B | C. | C | D. | D |
11.执行如图所示的程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( )
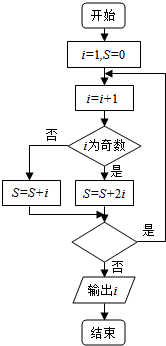

| A. | S≤10? | B. | S≤12? | C. | S≤14? | D. | S≤16? |
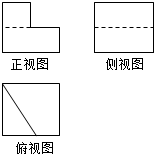
8.若某几何体的三视图如图所示,则这个几何体的直观图可以是( )

| A. | 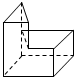 | B. | 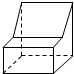 | C. | 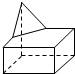 | D. |  |