题目内容
.(本小题满分12分)如图,在正方体 中,
中,
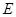 、
、 分别为棱
分别为棱 、
、 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)如果 ,一个动点从点
,一个动点从点 出发在正方体的
出发在正方体的
表面上依次经过棱 、
、 、
、 、
、 、
、 上的点,最终又回到点
上的点,最终又回到点 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.
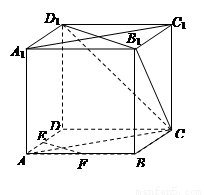
【答案】
(1)证明:连结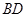 .
.
在正方体 中,对角线
中,对角线 .
.
又 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,
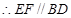 .
.
 .
…………2分
.
…………2分
又B1D1平面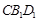 ,
,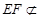 平面
平面 ,
,
 EF∥平面CB1D1.
…………4分
EF∥平面CB1D1.
…………4分
(2)证明: 在正方体
在正方体 中,AA1⊥平面A1B1C1D1,
中,AA1⊥平面A1B1C1D1,
而B1D1平面A1B1C1D1,

 AA1⊥B1D1.
AA1⊥B1D1.
又 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1,
 B1D1⊥平面CAA1C1. …………6分
B1D1⊥平面CAA1C1. …………6分
又 B1D1平面CB1D1,
B1D1平面CB1D1,
 平面CAA1C1⊥平面CB1D1.
…………8分
平面CAA1C1⊥平面CB1D1.
…………8分
(3)最小值为  .
…………9分
.
…………9分
如图,将正方体六个面展开成平面图形, …………10分
从图中F到F,两点之间线段最短,而且依次经过棱BB1、B1C1、C1D1、D1D、DA上的中点,所求的最小值为  .
…………12分.
.
…………12分.
【解析】略

练习册系列答案
相关题目