题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且四个顶点构成的四边形的面积是
,且四个顶点构成的四边形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且不垂直于
,且不垂直于![]() 轴,直线
轴,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 是坐标原点),若四边形
是坐标原点),若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)离心率提供![]() 与
与![]() 的关系,四个顶点构成的四边形对角线互相垂直,列出等量关系求
的关系,四个顶点构成的四边形对角线互相垂直,列出等量关系求![]() ,
,![]() 的值;
的值;
(2)直线![]() 经过点
经过点![]() ,由直线点斜式方程设出直线
,由直线点斜式方程设出直线![]() 的方程,并设出直线
的方程,并设出直线![]() 与椭圆
与椭圆![]() 交点
交点![]() 、
、![]() 的坐标,联立方程,由韦达定理可表示出
的坐标,联立方程,由韦达定理可表示出![]() 的中点
的中点![]() 的坐标;由中点
的坐标;由中点![]() 的坐标可得直线
的坐标可得直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程,利用韦达定理可求
的方程,利用韦达定理可求![]() ,再利用点到直线距离公式可求点
,再利用点到直线距离公式可求点![]() 、
、![]() 到直线
到直线![]() 的距离,由四边形
的距离,由四边形![]() 的面积为
的面积为![]() 可列出等量关系,最后可求出直线
可列出等量关系,最后可求出直线![]() 的方程.
的方程.
解:(1)由题意可得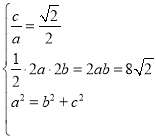 ,
,
解得![]() ,
,![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() .
.
联立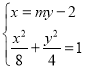 ,整理得
,整理得![]() ,
,
则![]() ,
,![]() ,
,
从而![]() ,故
,故![]() ,
,
直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
即![]() .
.
联立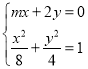 ,整理得
,整理得![]() ,
,
则![]() .
.
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则点
,则点![]() 到直线
到直线![]() 的距离也为
的距离也为![]() ,
,
从而![]() .
.
∵点![]() ,
,![]() 在直线
在直线![]() 的两侧,
的两侧,
∴![]() ,
,
∴![]() ,则
,则 ,
,
∵![]() ,
,
∴![]() ,
,
则四边形![]() 的面积
的面积![]() ,
,
∵四边形![]() 的面积为
的面积为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
故直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根据以上数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?
(参考公式:回归方程![]() ,其中
,其中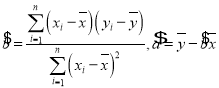 )
)