题目内容
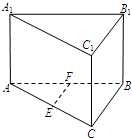 如图,在直棱柱ABC-A1B1C1中,AC=BC=4
如图,在直棱柱ABC-A1B1C1中,AC=BC=4| 3 |
| 20 |
| 3 |
| 28 |
| 3 |
| 20 |
| 3 |
| 28 |
| 3 |
分析:根据截面与平面ABC所成的二面角的大小为60°,故需要分类讨论,利用截面为梯形,可以计算各边长,从而可求截面的面积.
解答: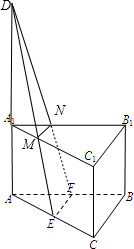 解:由题意,分类讨论:
解:由题意,分类讨论:
如右图,截面为MNFE,延长EM,CN,AA1,交于点D
∵直棱柱ABC-A1B1C1中,∠ACB=90°,E、F分别是AC、AB的中点
∴DE⊥EF
∴∠AED为截面与平面ABC所成的二面角
∴∠AED=60°
∵AE=
AC=2
∴DE=4
∵EF=
BC=2
∴S△DEF=
×4
×2
=12
∵DA=6,∴DA1=
DA
∴SDMN=
S△DEF=
∴截面的面积为12-
=
设截面EFN'M'在底面中的射影为EFPQ,则EF=2
,M'Q=2,CE=2
,∠M'EQ=60°
∴EQ=
∴PQ=
∴射影EFPQ的面积为
×(2
+
)×
=
∵截面与平面ABC所成的二面角的大小为60°
∴截面EFN'M'的面积为
÷cos60°=
故答案为:
或
 解:由题意,分类讨论:
解:由题意,分类讨论:如右图,截面为MNFE,延长EM,CN,AA1,交于点D
∵直棱柱ABC-A1B1C1中,∠ACB=90°,E、F分别是AC、AB的中点
∴DE⊥EF
∴∠AED为截面与平面ABC所成的二面角
∴∠AED=60°
∵AE=
| 1 |
| 2 |
| 3 |
∴DE=4
| 3 |
∵EF=
| 1 |
| 2 |
| 3 |
∴S△DEF=
| 1 |
| 2 |
| 3 |
| 3 |
∵DA=6,∴DA1=
| 2 |
| 3 |
∴SDMN=
| 4 |
| 9 |
| 16 |
| 3 |
∴截面的面积为12-
| 16 |
| 3 |
| 20 |
| 3 |
设截面EFN'M'在底面中的射影为EFPQ,则EF=2
| 3 |
| 3 |
∴EQ=
| 2 |
| 3 |
| 3 |
∴PQ=
| 8 |
| 3 |
| 3 |
∴射影EFPQ的面积为
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 14 |
| 3 |
∵截面与平面ABC所成的二面角的大小为60°
∴截面EFN'M'的面积为
| 14 |
| 3 |
| 28 |
| 3 |
故答案为:
| 20 |
| 3 |
| 28 |
| 3 |
点评:本题以直三棱柱为载体,考查截面面积的计算,搞清截面图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
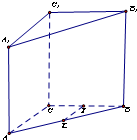 如图,在直棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=90°,AA1=2
如图,在直棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=90°,AA1=2 (2013•河西区一模)如图,在直棱柱ABC-A1B1C1中AB⊥BC,AB=BD=CC1=2,D为AC的中点.
(2013•河西区一模)如图,在直棱柱ABC-A1B1C1中AB⊥BC,AB=BD=CC1=2,D为AC的中点. (2009•临沂一模)如图,在直棱柱ABC-A1B1C1中,AC=BC=
(2009•临沂一模)如图,在直棱柱ABC-A1B1C1中,AC=BC=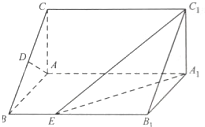 (2013•湖南)如图.在直棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=
(2013•湖南)如图.在直棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=