题目内容

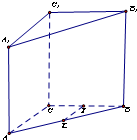如图，在直棱柱ABC-A1B1C1中，AC=BC=2，∠ACB=90°，AA1=2
3
，E，F分别为AB、CB中点，过直线EF作棱柱的截面，若截面与平面ABC所成的二面角的大小为60°，则截面的面积为（　　）
分析：根据截面与平面ABC所成的二面角的大小为60°，故需要分类讨论，利用
S射影
S截面
=cos60°，从而可求截面的面积．
解答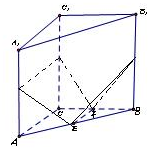：解：由题意，分类讨论：
如右图，当截面为三角形时，利用
S射影
S截面
=cos60°，
得
S△BEF
S截面
=cos60°，即
1
2
S截面
=
1
2
，
∴截面的面积为S=1；
当截面为四边形时，利用
S射影
S截面
=cos60°，
得
S四边形ACFE
S截面
=cos60°，即
3
2
S截面
=
1
2
，
∴截面的面积为S=3；
故选A．
点评：本题以直三棱柱为载体，考查截面面积的计算，搞清截面图形是解题的关键．
练习册系列答案
相关题目
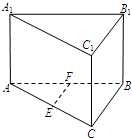如图，在直棱柱ABC-A1B1C1中，AC=BC=4
3
，∠ACB=90°，AA1=2，E、F分别是AC、AB的中点，过直线EF作棱柱的截面，若截面与平面ABC所成的二面角的大小为60°，则截面的面积为
20
3
或
28
3
（对一个给2分）
20
3
或
28
3
（对一个给2分）
．
（2013•河西区一模）如图，在直棱柱ABC-A1B1C1中AB⊥BC，AB=BD=CC1=2，D为AC的中点．
（I）证明AB1∥平面BDC1；
（Ⅱ）证明A1C⊥平面BDC1；
（Ⅲ）求二面角A-BC1-D的正切值．
（2009•临沂一模）如图，在直棱柱ABC-A1B1C1中，AC=BC=
12
AA1，∠ACB=90°，G为BB1的中点．
（Ⅰ）求证：平面A1CG⊥平面A1GC1；
（Ⅱ）求平面ABC与平面A1GC所成锐二面角的平面角的余弦值．
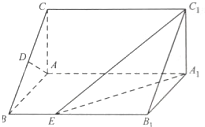（2013•湖南）如图．在直棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=
2
，AA1=3，D是BC的中点，点E在棱BB1上运动．
（1）证明：AD⊥C1E；
（2）当异面直线AC，C1E 所成的角为60°时，求三棱锥C1-A1B1E的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网