题目内容
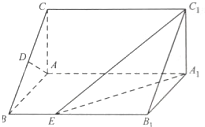 (2013•湖南)如图.在直棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=
(2013•湖南)如图.在直棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=| 2 |
(1)证明:AD⊥C1E;
(2)当异面直线AC,C1E 所成的角为60°时,求三棱锥C1-A1B1E的体积.
分析:(1)根据直三棱柱的性质,得AD⊥BB1,等腰△ABC中利用“三线合一”证出AD⊥BC,结合线面垂直判定定理,得AD⊥平面BB1C1C,从而可得AD⊥C1E;
(2)根据AC∥A1C1,得到∠EC1A1(或其补角)即为异面直线AC、C1E 所成的角.由A1C1⊥A1B1且A1C1⊥AA1,证出A1C1⊥平面AA1B1B,从而在Rt△A1C1E中得到∠EC1A1=60°,利用余弦的定义算出C1E=2A1C1=2
,进而得到△A1B1E面积为
,由此结合锥体体积公式即可算出三棱锥C1-A1B1E的体积.
(2)根据AC∥A1C1,得到∠EC1A1(或其补角)即为异面直线AC、C1E 所成的角.由A1C1⊥A1B1且A1C1⊥AA1,证出A1C1⊥平面AA1B1B,从而在Rt△A1C1E中得到∠EC1A1=60°,利用余弦的定义算出C1E=2A1C1=2
| 2 |
| 2 |
解答:解:(1)∵直棱柱ABC-A1B1C1中,BB1⊥平面ABC,AD?平面ABC,∴AD⊥BB1
∵△ABC中,AB=AC,D为BC中点,∴AD⊥BC
又∵BC、BB1?平面BB1C1C,BC∩BB1=B
∴AD⊥平面BB1C1C,结合C1E?平面BB1C1C,可得AD⊥C1E;
(2)∵直棱柱ABC-A1B1C1中,AC∥A1C1,
∴∠EC1A1(或其补角)即为异面直线AC、C1E 所成的角
∵∠BAC=∠B1A1C1=90°,∴A1C1⊥A1B1,
又∵AA1⊥平面A1B1C1,可得A1C1⊥AA1,
∴结合A1B1∩AA1=A1,可得A1C1⊥平面AA1B1B,
∵A1E?平面AA1B1B,∴A1C1⊥A1E
因此,Rt△A1C1E中,∠EC1A1=60°,可得cos∠EC1A1=
=
,得C1E=2A1C1=2
又∵B1C1=
=2,∴B1E=
=2
由此可得V C1-A1B1E=
S△ A1B1E×A1C1=
×
×2×
×
=
∵△ABC中,AB=AC,D为BC中点,∴AD⊥BC
又∵BC、BB1?平面BB1C1C,BC∩BB1=B
∴AD⊥平面BB1C1C,结合C1E?平面BB1C1C,可得AD⊥C1E;
(2)∵直棱柱ABC-A1B1C1中,AC∥A1C1,
∴∠EC1A1(或其补角)即为异面直线AC、C1E 所成的角
∵∠BAC=∠B1A1C1=90°,∴A1C1⊥A1B1,
又∵AA1⊥平面A1B1C1,可得A1C1⊥AA1,
∴结合A1B1∩AA1=A1,可得A1C1⊥平面AA1B1B,
∵A1E?平面AA1B1B,∴A1C1⊥A1E
因此,Rt△A1C1E中,∠EC1A1=60°,可得cos∠EC1A1=
| A 1C1 |
| C1E |
| 1 |
| 2 |
| 2 |
又∵B1C1=
| A1C12+A 1B12 |
| C 1E2-B1C12 |
由此可得V C1-A1B1E=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
点评:本题给出直三棱柱的底面是等腰直角三角形,在已知侧棱长和底面边长的情况下证明线线垂直并求锥体的体积,着重考查了直棱柱的性质、空间线面垂直的判定与性质等知识,属于中档题.

练习册系列答案
相关题目
 (2013•湖南)在等腰直角三角形ABC中,AB=AC=4,点P是边AB边上异于AB的一点,光线从点P出发,经BC,CA反射后又回到点P(如图1),若光线QR经过△ABC的重心,则AP等于( )
(2013•湖南)在等腰直角三角形ABC中,AB=AC=4,点P是边AB边上异于AB的一点,光线从点P出发,经BC,CA反射后又回到点P(如图1),若光线QR经过△ABC的重心,则AP等于( ) (2013•湖南)如图,在半径为
(2013•湖南)如图,在半径为 (2013•湖南)某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
(2013•湖南)某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示: (2013•湖南)如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.
(2013•湖南)如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.