Question

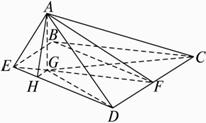
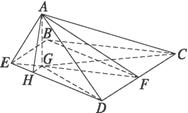
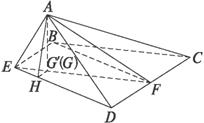
如图所示，二面角α-CD-β的大小为θ，点A在平面α内，△ACD的面积为s，且CD=m，过A点的直线交平面β于B，AB⊥CD，且AB与平面β所成的角为30°，则当θ=

60°

时，△BCD的面积取得最大值为

2S

．

Answer 1

分析：当BA⊥α于A时，△BCD的面积取得最大值．过A作AO⊥CD，连接BO，由AB⊥CD，知∠AOB是二面角α-CD-β的平面角，由AB与平面β所成的角为30°，知θ=∠AOB=60°．设△BCD的面积为S‘，由cos60°=

S

S′

，能求出△BCD的面积．

解答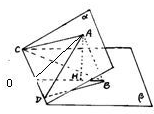：解：点A在平面α内，过A点的直线交平面β于B，
当BA⊥α于A时，△BCD的面积取得最大值．
过A作AO⊥CD，连接BO，
∵AB⊥CD，
∴∠AOB是二面角α-CD-β的平面角，
∵AB与平面β所成的角为30°，
∴θ=∠AOB=60°．
设△BCD的面积为S‘，
∵θ=∠AOB=60°，
∴cos60°=

S

S′

，
∴S′=2S．
故答案为：60°，2S．

点评：本题考查如何用面积法求二面角的大小，是基础题．解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题．