题目内容
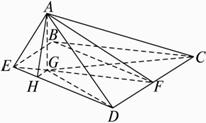
已知正方形ABCD,E、F分别是边AB、CD的中点,将△ADE沿DE折起,如图所示.记二面角ADEC的大小为θ(0<θ<π).(1)证明BF∥平面ADE;
(2)若△ACD为正三角形,试判断点A在平面BCDE内的射影G是否在直线EF上,证明你的结论,并求角θ的余弦值.
(1)证明:E、F分别是正方形ABCD的边AB、CD的中点,

∴EB∥FD,且EB=FD.
∴四边形EBFD是平行四边形.
∴BF∥ED.
∵ED![]() 平面AED,而BF
平面AED,而BF![]() 平面AED,
平面AED,
∴BF∥平面AED.
(2)解析一:一点A在平面BCDE内的射影G在直线EF上.
过点A作AG⊥平面BCDE,垂足为G,连结GC、GD.
∵△ACD为正三角形,
∴AC=AD,
∴GC=GD,
∴G在CD的垂直平分线上.
又∵EF是CD的垂直平分线,
∴点A在平面BCDE内的射影G在直线EF上.
过G作GH⊥ED,垂足为H,连结AH,则AH⊥DE,
∴∠AHG是二面角ADEC的平面角,即∠AHG=θ.
设原正方形ABCD的边长为2a,连结AF.
在折后图的△AEF中,AF=![]() a,EF=2AE=2a.
a,EF=2AE=2a.
∴△AEF为直角三角形,AG·EF=AE·AF.
∴AG=![]() a.
a.
在Rt△ADE中,AH·DE=AD·AE.
∴AH=![]() .∴GH=
.∴GH=![]() .
.
∴cosθ=![]() .
.
解析二:点A在平面BCDE内的射影G在直线EF上.
连结AF,在平面AEF内过点A作AG′⊥EF,垂足为G′.
∵△ACD为正三角形,F为CD的中点,
∴AF⊥CD.
又∵EF⊥CD,
∴CD⊥平面AEF.
∵AG′![]() 平面AEF,
平面AEF,
∴CD⊥AG′.
又∵AG′⊥EF,且CD∩EF=F,CD![]() 平面BCDE,EF
平面BCDE,EF![]() 平面BCDE,
平面BCDE,
∴AG′⊥平面BCDE.
∴G′为A在平面BCDE内的射影G.
∴点A在平面BCDE内的射影G在直线EF上.
过G作GH⊥ED,垂足为H,连结AH,则AH⊥DE.
∴∠AHG是二面角ADEC的平面角,即∠AHG=θ.
设原正方形ABCD的边长为2a.
在折后图的△AEF中,AF=![]() a,EF=2AE=2a.
a,EF=2AE=2a.
∴△AEF为直角三角形,AG·EF=AE·AF.
∴AG=![]() a.
a.
在Rt△ADE中,AH·DH=AD·AE.
∴AH=![]() .
.
∴GH=![]() .∴cosθ=
.∴cosθ=![]() =
=![]() .
.
解析三:点A在平面BCDE内的射影G在直线EF上.

连结AF,在平面AEF内过点A作AG′⊥EF,垂足为G′.
∵△ACD为正三角形,F为CD中点,
∴AF⊥CD.
又∵EF⊥CD,
∴CD⊥平面AEF.
∵CD![]() 平面BCDE,
平面BCDE,
∴平面AEF⊥平面BCDE.
又∵平面AEF∩平面BCDE=EF,AG′⊥EF,
∴AG′⊥平面BCDE,即G′为A在平面BCDE内的射影G,
∴点A在平面BCDE内的射影G在直线EF上.
过G作GH⊥DE,垂足为H,连结AH,则AH⊥DE.
∴∠AHG是二面角A-DE-C的平面角,即∠AHG=θ.
设原正方形ABCD的边长为2a.
在折后图的△AEF中,AF=![]() a,EF=2AE=2a.
a,EF=2AE=2a.
∴△AEF为直角三角形,AG·EF=AE·AF.
∴AG=![]() a.
a.
在Rt△ADE中,AH·DE=AD·AE.
∴AH=![]() .
.
∴GH=![]() .∴cosθ=
.∴cosθ=![]() .
.

| AB |
| BC |
| AC |
| A、0 | ||
| B、2 | ||
C、
| ||
D、2
|
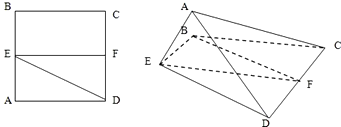 已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).
已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π). (2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
(2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,