题目内容
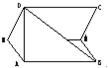ABCD是正方形，边长为7 cm，MN∥AB且交BC于点M，交DA于点N，若AN=3 cm，沿MN把正方形折成如图所示的二面角A-MN-D，大小为60°，求图中异面直线MN与BD间的距离．
分析：由题意易证MN∥平面ABD，MN与BD的距离可转化为点N到平面ABD的距离，作NE⊥AD，易证NE⊥平面ABD，故可求NE．
解答：解：由题意可知∵MN∥AB，MN?平面ABD，AB?平面ABD
∴MN∥平面ABD，
∴MN与BD的距离可转化为点N到平面ABD的距离，
作NE⊥AD，∵NE⊥AB，AD∩AB=A
∴NE⊥平面ABD，
故可求NE=
．
∴MN∥平面ABD，
∴MN与BD的距离可转化为点N到平面ABD的距离，
作NE⊥AD，∵NE⊥AB，AD∩AB=A
∴NE⊥平面ABD，
故可求NE=
6
| ||
| 13 |
点评：本小题主要考查异面直线的距离，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
相关题目
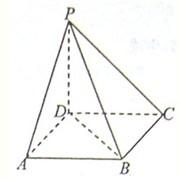如图所示，已知ABCD是正方形，边长为2，PD⊥平面ABCD．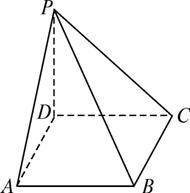
，且PD是四棱锥的高． 
，PD=