题目内容
已知动点P在曲线2x2-y=0上移动,则点A(0,-1)与点P连线中点的轨迹方程是
8x2-2y-1=0
8x2-2y-1=0
.分析:设出点A(0,-1)与点P连线中点的坐标,利用中点坐标公式可得P(2x,2y+1),根据动点P在曲线2x2-y=0上移动,代入方程即可求得点A(0,-1)与点P连线中点的轨迹方程
解答:解:设点A(0,-1)与点P连线中点坐标为(x,y),则由中点坐标公式可得P(2x,2y+1),
∵动点P在曲线2x2-y=0上移动,
∴2(2x)2-(2y+1)=0
即8x2-2y-1=0
故答案为:8x2-2y-1=0.
∵动点P在曲线2x2-y=0上移动,
∴2(2x)2-(2y+1)=0
即8x2-2y-1=0
故答案为:8x2-2y-1=0.
点评:本题考查轨迹方程的求法,考查中点坐标公式,考查代入法的运用,解题的关键是确定动点坐标之间的关系.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
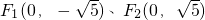 ,动点P满足条件:
,动点P满足条件: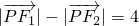 ,设点P的轨迹是曲线E,O为坐标原点.
,设点P的轨迹是曲线E,O为坐标原点.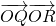 的取值范围;
的取值范围;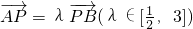 ,记xA、xB分别为A、B两点的横坐标,求|xA•xB|的最小值.
,记xA、xB分别为A、B两点的横坐标,求|xA•xB|的最小值. ;
; ,O为坐标原点,则动点P的轨迹为圆;
,O为坐标原点,则动点P的轨迹为圆;