题目内容
已知平面内两定点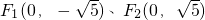 ,动点P满足条件:
,动点P满足条件: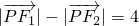 ,设点P的轨迹是曲线E,O为坐标原点.
,设点P的轨迹是曲线E,O为坐标原点.
(I)求曲线E的方程;
(II)若直线y=k(x+1)与曲线E相交于两不同点Q、R,求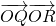 的取值范围;
的取值范围;
(III)(文科做)设A、B两点分别在直线y=±2x上,若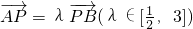 ,记xA、xB分别为A、B两点的横坐标,求|xA•xB|的最小值.
,记xA、xB分别为A、B两点的横坐标,求|xA•xB|的最小值.
(理科做)设A、B两点分别在直线y=±2x上,若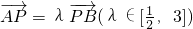 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
解:(I)由题意,可知动点P的轨迹是焦点在y轴上的双曲线的上半支,
其中c= ,2a=4,
,2a=4,
∴b=1,
∴曲线E的方程是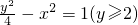 .
.
(II)设Q(x1,y1),R(x2,y2),(y1,y2>0),
由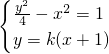 ,得
,得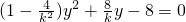 ,
,
当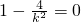 ,即k=±2时,显然不符合题意,
,即k=±2时,显然不符合题意,
∴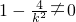 .
.
∴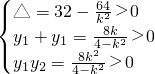 ,
,
解得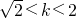 .
.
∵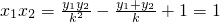 ,
,
∴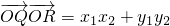
=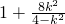
=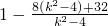
=-7+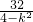 .
.
∵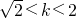 ,
,
∴0<4-k2<2,
∴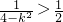 ,
,
∴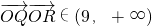 .
.
(III)(文科做)∵曲线E的方程是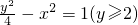 ,
,
∴双曲线的两条渐近线方程为y=±2x.
∵ ,且λ>0,
,且λ>0,
∴点P必内分线段AB,
故点A,B均在x轴上方,
不妨设xA>0,xB<0,
即A(xA,2xA),B(xB,-2xB),
由 ,得P点的坐标为(
,得P点的坐标为(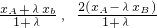 ),
),
将P点坐标代入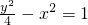 中,
中,
化简,得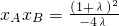 =
=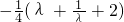 .
.
∴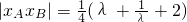 ,
,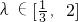
∵ ,当且仅当λ=1时,等号成立.
,当且仅当λ=1时,等号成立.
∴|xA•xB|min=1.
(理科做))∵曲线E的方程是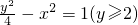 ,
,
∴双曲线的两条渐近线方程为y=±2x.
∵ ,且λ>0,
,且λ>0,
∴点P必内分线段AB,
故点A,B均在x轴上方,
设A(m,2m),B(-n,2n),m>0.n>0.
由 ,得点P的坐标为(
,得点P的坐标为(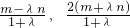 ).
).
将点P的从标代入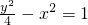 中,
中,
化简,得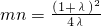 .
.
设∠AOB=2θ,
∵tan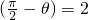 ,
,
∴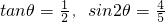 ,
,
∵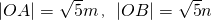 ,
,
∴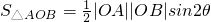
=2mn
=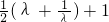 .
.
∵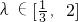 ,
,
∴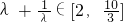 ,
,
∴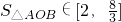 .
.
∴△ABC面积的最大值为 .
.
分析:(I)由题意,可知动点P的轨迹是焦点在y轴上的双曲线的上半支,其中c= ,2a=4,由此能求出曲线E的方程.
,2a=4,由此能求出曲线E的方程.
(II)设Q(x1,y1),R(x2,y2),(y1,y2>0),由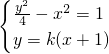 ,得
,得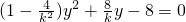 ,当
,当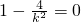 ,不符合题意,故
,不符合题意,故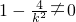 .由此入手能够求出求
.由此入手能够求出求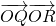 的取值范围.
的取值范围.
(III)(文科做)由曲线E的方程是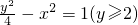 ,知双曲线的两条渐近线方程为y=±2x.由
,知双曲线的两条渐近线方程为y=±2x.由 ,且λ>0,知点A,B均在x轴上方,设A(xA,2xA),B(xB,-2xB),由
,且λ>0,知点A,B均在x轴上方,设A(xA,2xA),B(xB,-2xB),由 ,得P点的坐标为(
,得P点的坐标为(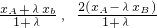 ),将P点坐标代入
),将P点坐标代入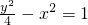 中,得
中,得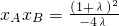 =
=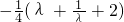 .由此能求出|xA•xB|的最小值.
.由此能求出|xA•xB|的最小值.
(理科做))由曲线E的方程是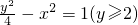 ,知双曲线的两条渐近线方程为y=±2x.由
,知双曲线的两条渐近线方程为y=±2x.由 ,且λ>0,知点A,B均在x轴上方,设A(m,2m),B(-n,2n),m>0.n>0.由
,且λ>0,知点A,B均在x轴上方,设A(m,2m),B(-n,2n),m>0.n>0.由 ,得点P的坐标为(
,得点P的坐标为(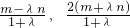 ).将P的从标代入
).将P的从标代入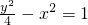 中,得
中,得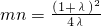 .设∠AOB=2θ,由
.设∠AOB=2θ,由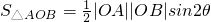 ,由此能求出△ABC面积的最大值.
,由此能求出△ABC面积的最大值.
点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答
其中c=
 ,2a=4,
,2a=4,∴b=1,
∴曲线E的方程是
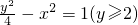 .
.(II)设Q(x1,y1),R(x2,y2),(y1,y2>0),
由
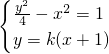 ,得
,得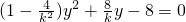 ,
,当
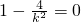 ,即k=±2时,显然不符合题意,
,即k=±2时,显然不符合题意,∴
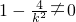 .
.∴
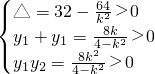 ,
,解得
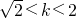 .
.∵
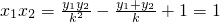 ,
,∴
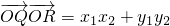
=
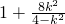
=
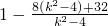
=-7+
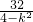 .
.∵
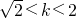 ,
,∴0<4-k2<2,
∴
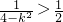 ,
,∴
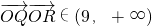 .
.(III)(文科做)∵曲线E的方程是
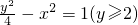 ,
,∴双曲线的两条渐近线方程为y=±2x.
∵
 ,且λ>0,
,且λ>0,∴点P必内分线段AB,
故点A,B均在x轴上方,
不妨设xA>0,xB<0,
即A(xA,2xA),B(xB,-2xB),
由
 ,得P点的坐标为(
,得P点的坐标为(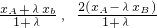 ),
),将P点坐标代入
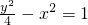 中,
中,化简,得
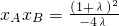 =
=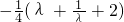 .
.∴
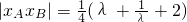 ,
,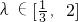
∵
 ,当且仅当λ=1时,等号成立.
,当且仅当λ=1时,等号成立.∴|xA•xB|min=1.
(理科做))∵曲线E的方程是
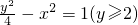 ,
,∴双曲线的两条渐近线方程为y=±2x.
∵
 ,且λ>0,
,且λ>0,∴点P必内分线段AB,
故点A,B均在x轴上方,
设A(m,2m),B(-n,2n),m>0.n>0.
由
 ,得点P的坐标为(
,得点P的坐标为(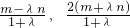 ).
).将点P的从标代入
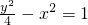 中,
中,化简,得
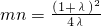 .
.设∠AOB=2θ,
∵tan
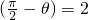 ,
,∴
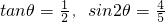 ,
,∵
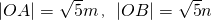 ,
,∴
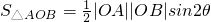
=2mn
=
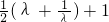 .
.∵
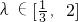 ,
,∴
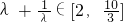 ,
,∴
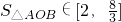 .
.∴△ABC面积的最大值为
 .
.分析:(I)由题意,可知动点P的轨迹是焦点在y轴上的双曲线的上半支,其中c=
 ,2a=4,由此能求出曲线E的方程.
,2a=4,由此能求出曲线E的方程.(II)设Q(x1,y1),R(x2,y2),(y1,y2>0),由
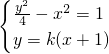 ,得
,得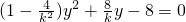 ,当
,当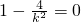 ,不符合题意,故
,不符合题意,故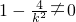 .由此入手能够求出求
.由此入手能够求出求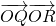 的取值范围.
的取值范围.(III)(文科做)由曲线E的方程是
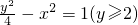 ,知双曲线的两条渐近线方程为y=±2x.由
,知双曲线的两条渐近线方程为y=±2x.由 ,且λ>0,知点A,B均在x轴上方,设A(xA,2xA),B(xB,-2xB),由
,且λ>0,知点A,B均在x轴上方,设A(xA,2xA),B(xB,-2xB),由 ,得P点的坐标为(
,得P点的坐标为(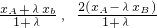 ),将P点坐标代入
),将P点坐标代入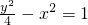 中,得
中,得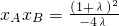 =
=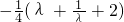 .由此能求出|xA•xB|的最小值.
.由此能求出|xA•xB|的最小值.(理科做))由曲线E的方程是
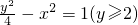 ,知双曲线的两条渐近线方程为y=±2x.由
,知双曲线的两条渐近线方程为y=±2x.由 ,且λ>0,知点A,B均在x轴上方,设A(m,2m),B(-n,2n),m>0.n>0.由
,且λ>0,知点A,B均在x轴上方,设A(m,2m),B(-n,2n),m>0.n>0.由 ,得点P的坐标为(
,得点P的坐标为(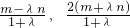 ).将P的从标代入
).将P的从标代入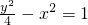 中,得
中,得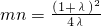 .设∠AOB=2θ,由
.设∠AOB=2θ,由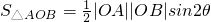 ,由此能求出△ABC面积的最大值.
,由此能求出△ABC面积的最大值.点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
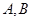 及动点
及动点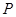 ,设命题甲是:“
,设命题甲是:“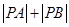 是定值”,命题乙是:“点
是定值”,命题乙是:“点 及动点
及动点 ,设命题甲是:“
,设命题甲是:“ 是定值”,命题乙是:“点
是定值”,命题乙是:“点 及动点
及动点 ,设命题甲是:“
,设命题甲是:“ 是定值”,命题乙是:“点
是定值”,命题乙是:“点