题目内容
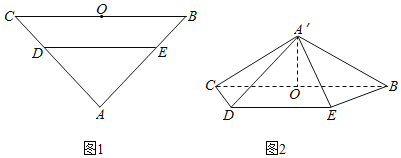
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得
折起,使得![]() .
.
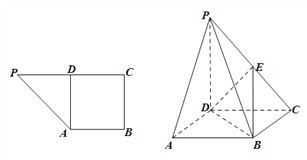
(Ⅰ)若![]() 是
是![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析: ![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,推导出
,推导出![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;
; ![]() 推导出
推导出![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;
; ![]() 以
以![]() 为原点,以
为原点,以![]() 所在的直线分别为
所在的直线分别为![]() 轴
轴![]() 轴,
轴, ![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,利用向量法能求出二面角
,利用向量法能求出二面角![]() 的大小
的大小
解析:(Ⅰ)证明:连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
在正方形![]() 中,
中, ![]() 为
为![]() 中点,又因为
中点,又因为![]() 为
为![]() 中点,
中点,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)由已知可得![]()
又因为![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以平面![]() 平面
平面![]()
解:(Ⅲ)由(Ⅱ)知, ![]() 平面
平面![]() 所以
所以![]() ,又因为
,又因为![]()
所以![]() 平面
平面![]()
所以以![]() 为原点,以
为原点,以![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
则点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
所以![]() 即
即![]()
令![]() ,解得
,解得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
所以![]() 即
即![]()
令![]() ,解得
,解得![]() .
.
所以![]() .
.
由图可知,二面角![]() 为钝角,所以二面角
为钝角,所以二面角![]() 的大小为
的大小为![]() .
.

【题目】节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的产品为优质品.现用A,B两种不同型号的节能灯做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示.
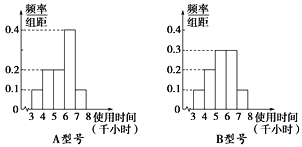
以上述试验结果中使用时间落入各组的频率作为相应的概率.
(1)现从大量的A,B两种型号节能灯中各随机抽取两件产品,求恰有两件是优质品的概率;
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”.通过多年统计发现,A型节能灯每件产品的利润y(单位:元)与其使用时间t(单位:千小时)的关系如下表:
使用时间t(单位:千小时) | t<4 | 4≤t<6 | t≥6 |
每件产品的利润y(单位:元) | -10 | 10 | 20 |
若从大量的A型节能灯中随机抽取两件,其利润之和记为X(单位:元),求X的分布列及数学期望.