题目内容
(本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的定义域;
的定义域;
(Ⅱ)若关于 的不等式
的不等式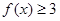 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.
【答案】
(Ⅰ)函数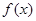 的定义域为
的定义域为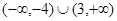 ;(Ⅱ)
;(Ⅱ)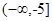 .
.
【解析】
试题分析:(Ⅰ)由题设知: ,
,
不等式的解集是以下不等式组解集的并集:
 ,或
,或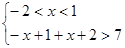 ,或
,或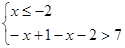 ………………3分
………………3分
解得函数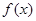 的定义域为
的定义域为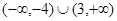 ; ………………………………5分
; ………………………………5分
(Ⅱ)不等式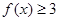 即
即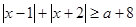 ,
,
 时,恒有
时,恒有 ,…………………………8分
,…………………………8分
 不等式
不等式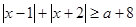 解集是R,
解集是R,
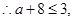
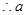 的取值范围是
的取值范围是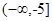 .
……………………………10分
.
……………………………10分
考点:本题主要考查对数函数的性质,绝对值不等式的解法。
点评:中档题,解含绝对值不等式的基本方法,是“去绝对值符号”,思路一般有:平方法、分类讨论法或利用绝对值的几何意义。(II)实际上是一个恒成立问题,转化成求函数最值后,利用绝对值不等式的性质得解。

练习册系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,