题目内容
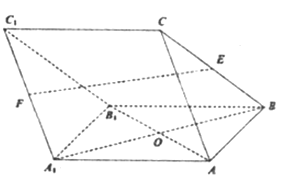
【题目】如图,等高的正三棱锥P-ABC与圆锥SO的底面都在平面M上,且圆O过点A,又圆O的直径AD⊥BC,垂足为E,设圆锥SO的底面半径为1,圆锥体积为![]() 。
。
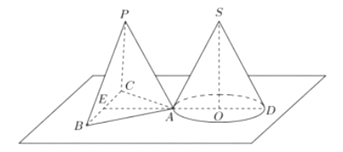
(1)求圆锥的侧面积;
(2)求异面直线AB与SD所成角的大小;
(3)若平行于平面M的一个平面N截得三棱锥与圆锥的截面面积之比为![]() ,求三棱锥的侧棱PA与底面ABC所成角的大小。
,求三棱锥的侧棱PA与底面ABC所成角的大小。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用圆锥体积可求得圆锥的高,进而得到母线长,根据圆锥侧面积公式可求得结果;(2)作![]() 交圆锥底面圆于点
交圆锥底面圆于点![]() ,则
,则![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,在
所成角,在![]() 中,求解出三边长,利用余弦定理可求得
中,求解出三边长,利用余弦定理可求得![]() ,从而得到结果;(3)根据截面面积之比可得底面积之比,求得
,从而得到结果;(3)根据截面面积之比可得底面积之比,求得![]() ,进而求得等边三角形的边长,利用正棱锥的特点可知若
,进而求得等边三角形的边长,利用正棱锥的特点可知若![]() 为
为![]() 的中心,则
的中心,则![]() 即为侧棱
即为侧棱![]() 与底面
与底面![]() 所成角,在
所成角,在![]() 中利用正切值求得结果.
中利用正切值求得结果.
(1)设圆锥高为![]() ,母线长为
,母线长为![]()
由圆锥体积得:![]()
![]()
![]()
![]() 圆锥的侧面积:
圆锥的侧面积:![]()
(2)作![]() 交圆锥底面圆于点
交圆锥底面圆于点![]() ,连接
,连接![]() ,
,![]()
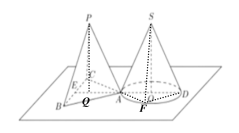
则![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角
所成角
由题意知:![]() ,
,![]()
![]() ,又
,又![]()
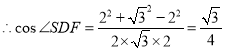
![]()
即异面直线![]() 与
与![]() 所成角为:
所成角为:![]()
(3)![]() 平行于平面M的一个平面N截得三棱锥与圆锥的截面面积之比为
平行于平面M的一个平面N截得三棱锥与圆锥的截面面积之比为![]()

![]()
又![]()
![]() ,即
,即![]() 为边长为
为边长为![]() 的等边三角形
的等边三角形
设![]() 为
为![]() 的中心,连接
的中心,连接![]() ,则
,则![]()
三棱锥![]() 为正三棱锥
为正三棱锥 ![]() 平面
平面![]()
![]() 即为侧棱
即为侧棱![]() 与底面
与底面![]() 所成角
所成角
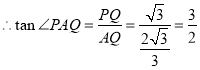
![]()
即侧棱![]() 与底面
与底面![]() 所成角为:
所成角为:![]()

【题目】某消费品企业销售部对去年各销售地的居民年收入(即此地所有居民在一年内的收入的总和)及其产品销售额进行抽样分析,收集数据整理如下:
销售地 | A | B | C | D |
年收入x(亿元) | 15 | 20 | 35 | 50 |
销售额y(万元) | 16 | 20 | 40 | 48 |
(1)在图a中作出这些数据的散点图,并指出y与x成正相关还是负相关?
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程?
(3)若B地今年的居民年收入将增长20%,预测B地今年的销售额将达到多少万元?
回归方程系数公式: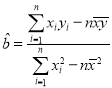 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.