题目内容
14、已知函数f（x）=|x|-1，关于x的方程f2（x）-|f（x）|+k=0，给出下列四个命题：
①存在实数k，使得方程恰有2个不同的实根；
②存在实数k，使得方程恰有4个不同的实根；
③存在实数k，使得方程恰有5个不同的实根；
④存在实数k，使得方程恰有8个不同的实根．
其中真命题的序号为
①存在实数k，使得方程恰有2个不同的实根；
②存在实数k，使得方程恰有4个不同的实根；
③存在实数k，使得方程恰有5个不同的实根；
④存在实数k，使得方程恰有8个不同的实根．
其中真命题的序号为
①②③④
．分析：将方程f2（x）-|f（x）|+k=0，的问题转化成函数f2（x）-|f（x）|=-k，图象的问题，画出可得．
解答：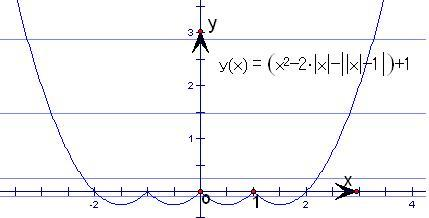
解：关于x的方程f2（x）-|f（x）|+k=0，可化为f2（x）-|f（x）|=-k，
分别画出函数y=f2（x）-|f（x）|和y=-k的图象，如图．
由图可知，它们的交点情况是：
恰有2，4，5，8个不同的交点
故答案为：①②③④．
解：关于x的方程f2（x）-|f（x）|+k=0，可化为f2（x）-|f（x）|=-k，分别画出函数y=f2（x）-|f（x）|和y=-k的图象，如图．
由图可知，它们的交点情况是：
恰有2，4，5，8个不同的交点
故答案为：①②③④．
点评：本题考查了分段函数，以及函数与方程的思想，数形结合的思想．
练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|