题目内容
函数![]() 的定义域为
的定义域为![]() ,并满足条件
,并满足条件
① 对任意![]() ,有
,有![]() ;
;
② 对任意![]() ,有
,有![]() ;
;
③ ![]() .
.
(1)求![]() 的值;
的值;
![]() (2)求证:
(2)求证:![]() 在
在![]() 上是单调递增函数;
上是单调递增函数;
(3)若![]() ,且
,且![]() ,求证
,求证![]() .
.
1
解析:
解法一:(1)令![]() ,则
,则![]()
![]()
(2)任取![]() ,且
,且![]()
设![]() ,则
,则![]()
![]()
![]() ,
,![]()
![]() ,
,![]() 在
在![]() 上是单调递增函数
上是单调递增函数
(3)由(1)(2)知![]() ,
,![]()
![]()
![]()
又![]() ,
,![]()
![]()
![]()
解法二:(1)![]() 对任意
对任意![]() ,有
,有![]()
![]()
![]() 当
当![]() 时,
时,![]()
![]() ,
,![]() ,
,![]()
(2)![]() ,
,![]()
![]() 是
是![]() 上的单调增函数
上的单调增函数
![]() 在
在![]() 上是单调递增函数
上是单调递增函数
(3)![]()
而![]() ,
,![]()
![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 的定义域为
的定义域为 ,并满足以下条件:①对任意
,并满足以下条件:①对任意 ,有
,有 ;②对任意
;②对任意 ,有
,有 ;③
;③ .
. 的值;
的值; ,且
,且 ,求证:
,求证: .
. 的定义域为
的定义域为 ,并满足以下三个条件:(i)对任意
,并满足以下三个条件:(i)对任意 ,有
,有 ;
; ,有
,有 ;(iii)
;(iii) 。
。 的值;
的值; ,且
,且 ,求证:
,求证: 。
。 的定义域为
的定义域为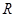 ,并满足以下条件:①对任意的
,并满足以下条件:①对任意的 ;
; ,都有
,都有 ;③
;③ .
. 的值;
的值; 是
是 上的单调递增函数;
上的单调递增函数; 的不等式:
的不等式: