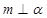题目内容
如图,AB、CD均为圆O的直径,CE⊥圆O所在的平面,BF∥CE.求证:
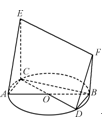
(1)平面BCEF⊥平面ACE;
(2)直线DF∥平面ACE.

(1)平面BCEF⊥平面ACE;
(2)直线DF∥平面ACE.
(1)见解析(2)见解析
证明:(1)因为CE⊥圆O所在的平面,BC 圆O所在的平面,所以CE⊥BC.
圆O所在的平面,所以CE⊥BC.
因为AB为圆O的直径,点C在圆O上,所以AC⊥BC,
因为AC∩CE=C,AC,CE 平面ACE,所以BC⊥平面ACE,
平面ACE,所以BC⊥平面ACE,
因为BC 平面BCEF,所以平面BCEF⊥平面ACE.
平面BCEF,所以平面BCEF⊥平面ACE.
(2)由(1)AC⊥BC,又因为CD为圆O的直径,所以BD⊥BC,
因为AC、BC、BD在同一平面内,所以AC∥BD,
因为BD 平面ACE,AC
平面ACE,AC 平面ACE,所以BD∥平面ACE.
平面ACE,所以BD∥平面ACE.
因为BF∥CE,同理可证BF∥平面ACE,
因为BD∩BF=B,BD、BF 平面BDF,所以平面BDF∥平面ACE,
平面BDF,所以平面BDF∥平面ACE,
因为DF 平面BDF,所以DF∥平面ACE
平面BDF,所以DF∥平面ACE
 圆O所在的平面,所以CE⊥BC.
圆O所在的平面,所以CE⊥BC.因为AB为圆O的直径,点C在圆O上,所以AC⊥BC,
因为AC∩CE=C,AC,CE
 平面ACE,所以BC⊥平面ACE,
平面ACE,所以BC⊥平面ACE,因为BC
 平面BCEF,所以平面BCEF⊥平面ACE.
平面BCEF,所以平面BCEF⊥平面ACE.(2)由(1)AC⊥BC,又因为CD为圆O的直径,所以BD⊥BC,
因为AC、BC、BD在同一平面内,所以AC∥BD,
因为BD
 平面ACE,AC
平面ACE,AC 平面ACE,所以BD∥平面ACE.
平面ACE,所以BD∥平面ACE.因为BF∥CE,同理可证BF∥平面ACE,
因为BD∩BF=B,BD、BF
 平面BDF,所以平面BDF∥平面ACE,
平面BDF,所以平面BDF∥平面ACE,因为DF
 平面BDF,所以DF∥平面ACE
平面BDF,所以DF∥平面ACE
练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的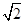 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.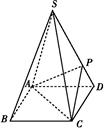
 AD=2,CD=3,直线PA与底面ABCD所成角为60°,点M、N分别是PA、PB的中点.求证:
AD=2,CD=3,直线PA与底面ABCD所成角为60°,点M、N分别是PA、PB的中点.求证: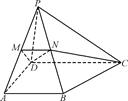
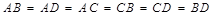 ,则
,则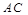 与
与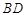 所成角为( )
所成角为( )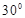
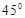
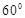
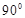
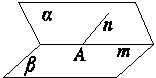
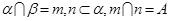
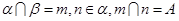
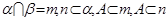
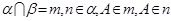
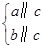 a∥b;②
a∥b;②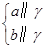 a∥b;③
a∥b;③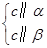 α∥β;
α∥β;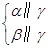 α∥β;⑤
α∥β;⑤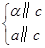 α∥a;⑥
α∥a;⑥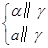 a∥α.
a∥α.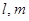 是两条不同的直线,
是两条不同的直线,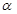 是一个平面,且
是一个平面,且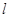 ∥
∥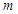 ,则
,则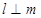 ,则
,则