题目内容
下列四个命题中
①“k=1”是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件;
②“a=3”是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直”的充要条件;
③函数y=
的最小值为2
其中假命题的为______将你认为是假命题的序号都填上)
①“k=1”是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件;
②“a=3”是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直”的充要条件;
③函数y=
| x2+4 | ||
|
其中假命题的为______将你认为是假命题的序号都填上)
①当k=-1,函数y=cos2(-x)-sin2(-x)=cos2x,最小正周期也为π,是个假命题;
②直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直,
根据两条线垂直的充要条件3a+2(a-1)=0,得到a=
,这是一个假命题;
③函数 y=
=
=
+
≥2,
等号不能成立,不能取到最小值,
综上可知假命题有①②③,
故答案为:①②③.
②直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直,
根据两条线垂直的充要条件3a+2(a-1)=0,得到a=
| 2 |
| 5 |
③函数 y=
| x2+4 | ||
|
| x2+3+1 | ||
|
| x 2+3 |
| 1 | ||
|
等号不能成立,不能取到最小值,
综上可知假命题有①②③,
故答案为:①②③.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
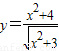 的最小值为2
的最小值为2