题目内容
下列四个命题中
①“k=1”是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件;
②“a=3”是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直”的充要条件;
③函数y=
的最小值为2
其中假命题的为
①“k=1”是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件;
②“a=3”是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直”的充要条件;
③函数y=
| x2+4 | ||
|
其中假命题的为
①②③
①②③
(将你认为是假命题的序号都填上)分析:①将f(x)恒等变形后,分析可得“k=±1”是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件,②根据两条线垂直的充要条件写出斜率乘积等于-1,得到a的值,③函数整理出来满足基本不等式的形式,但是等号不能成立.综合可得答案.
解答:解:①y=cos2kx-sin2kx=cos2kx,最小正周期为π,则k=±1,即①“k=±1”是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件,①是个假命题;
②若直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直,根据两条线垂直的充要条件,可得3a+2(a-1)=0,解可得a=
,这是一个假命题;
③函数 y=
=
=
+
,由于
≥
,则
+
≥
>2,
③是假命题,
综上可知假命题有①②③,
故答案为:①②③.
②若直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直,根据两条线垂直的充要条件,可得3a+2(a-1)=0,解可得a=
| 2 |
| 5 |
③函数 y=
| x2+4 | ||
|
| x2+3+1 | ||
|
| x 2+3 |
| 1 | ||
|
| x2+3 |
| 3 |
| x 2+3 |
| 1 | ||
|
4
| ||
| 3 |
③是假命题,
综上可知假命题有①②③,
故答案为:①②③.
点评:本题考查的知识点是命题的真假判断,其中根据基本知识点判断出题目中命题的真假是解答本题的关键,本题涉及到的知识点比较多,需要认真分析.

练习册系列答案
相关题目
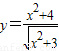 的最小值为2
的最小值为2