题目内容
若函数f(x)是R上的增函数,且恒有f(x)>0,设F(x)=
思路解析:利于单调性定量化定义证明的关键是推证F(x1)和F(x2)的大小.
证明:在区间R上任意选取x1,x2,且x1<x2.∵f(x)是区间R上的增函数,
∴f(x1)<f(x2).又∵f(x)>0,∴0<f(x1)<f(x2).∴![]() >
>![]() >0,即F(x1)>F(x2).∴函数F(x)=
>0,即F(x1)>F(x2).∴函数F(x)= ![]() 是R上的增函数.
是R上的增函数.
误区警示
在利用函数单调性的定量化定义证明函数的单调性时,虽然“作差”是我们比较大小的一种重要且常用的方法,但是,“作差”也仅是我们比较大小的一种手段,而不是目的,比较大小才是我们的目的.因此,比较大小不一定“作差”,还可以利用不等式的性质比较大小,以及“作商”等方法.

练习册系列答案
相关题目
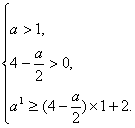 是R上的增函数,则实数a的取值范围为( )
是R上的增函数,则实数a的取值范围为( )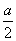 是R上的单调递增函数,则实数a的取值范围为
是R上的单调递增函数,则实数a的取值范围为