题目内容
设(2x－1)6＝a6x6＋a5x5＋…＋a1x＋a0，则|a0|＋|a1|＋|a2|＋…＋|a6|＝________.
729
∵Tr＋1＝
(2x)6－r(－1)r＝(－1)r26－rx6－r，
∴ar＋1＝(－1)r26－r，
∴|a0|＋|a1|＋|a2|＋…＋|a6|
＝a0－a1＋a2－a3＋a4－a5＋a6
＝[2×(－1)－1]6＝36＝729.
(2x)6－r(－1)r＝(－1)r26－rx6－r，∴ar＋1＝(－1)r26－r
，∴|a0|＋|a1|＋|a2|＋…＋|a6|
＝a0－a1＋a2－a3＋a4－a5＋a6
＝[2×(－1)－1]6＝36＝729.
练习册系列答案
相关题目
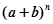的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和.
－
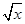)n的展开式中，前三项系数的绝对值依次成等差数列．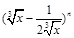
的展开式中，第6项
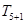为常数项.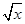
＋
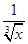)24的展开式中，x的幂指数是整数的项共有( )
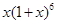的展开式中，含
项的系数为（ ）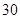
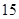
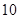
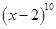的展开式中第5项的二项式系数是（ ） 
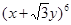的二项展开式中，
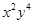项的系数是（ ）