题目内容
4.正项等比数列{an}满足a3=a2+2a1,且a4=24.(1)求an;
(2)若数列{an•bn}的前n项和Tn=3n•2n+1,求bn.
分析 (1)通过a3=a2+2a1可知q2-q-2=0,解得q=2,通过${a}_{1}{q}^{3}$=24可知a1=3,进而计算可得结论;
(2)通过an•bn=Tn-Tn-1=3(n+1)•2n可知bn=2(n+1)(n≥2),进而可得结论.
解答 解:(1)∵a3=a2+2a1,
∴a1q2=a1q+2a1,
∴q2-q-2=0,
解得:q=2或q=-1(舍),
又∵a4=24,即${a}_{1}{q}^{3}$=24,
∴a1=$\frac{24}{{2}^{3}}$=3,
∴an=3•2n-1;
(2)∵an•bn=Tn-Tn-1
=3n•2n+1-3(n-1)•2n
=3(n+1)•2n(n≥2),
∴bn=$\frac{3(n+1)•{2}^{n}}{{a}_{n}}$
=$\frac{3(n+1)•{2}^{n}}{3•{2}^{n-1}}$
=2(n+1)(n≥2),
又∵b1=$\frac{{T}_{1}}{{a}_{1}}$=$\frac{3•{2}^{2}}{3}$=4满足上式,
∴bn=2(n+1).
点评 本题考查数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

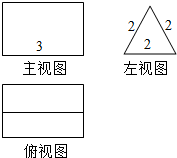 如图是一个柱体的三视图,它的体积等于底面积乘以高,该柱体的体积等于3$\sqrt{3}$.
如图是一个柱体的三视图,它的体积等于底面积乘以高,该柱体的体积等于3$\sqrt{3}$.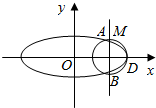 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为2,离心率e=$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为2,离心率e=$\frac{\sqrt{2}}{2}$.