题目内容
不等式sinx<0,x∈[-
,
π]的解集为
| π |
| 2 |
| 3 |
| 2 |
[-
,0)∪(π,
π])
| π |
| 2 |
| 3 |
| 2 |
[-
,0)∪(π,
π])
.| π |
| 2 |
| 3 |
| 2 |
分析:先画出函数y=sinx x∈[-
,
π]的图象,再数形结合即可得所求不等式的解集
| π |
| 2 |
| 3 |
| 2 |
解答:解: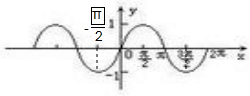 函数y=sinx x∈[-
函数y=sinx x∈[-
,
π]的图象如图:
数形结合可得sinx<0的解集为[-
,0)∪(π,
π])
故答案为[-
,0)∪(π,
π])
 函数y=sinx x∈[-
函数y=sinx x∈[-| π |
| 2 |
| 3 |
| 2 |
数形结合可得sinx<0的解集为[-
| π |
| 2 |
| 3 |
| 2 |
故答案为[-
| π |
| 2 |
| 3 |
| 2 |
点评:本题考察了简单三角不等式的解法,解决此类问题一定要将三角函数的图象牢记心中,学会运用数形结合的思想解决问题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知f(x)是定义在(-3,3)上的偶函数,当0<x<3时,f(x)的图象如下图所示,那么不等式f(x)sinx<0的解集是( )
已知f(x)是定义在(-3,3)上的偶函数,当0<x<3时,f(x)的图象如下图所示,那么不等式f(x)sinx<0的解集是( ) ,
, π]的解集为________.
π]的解集为________.