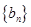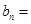题目内容
等差数列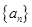 前
前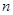 项和
项和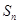 ,若
,若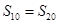 ,则
,则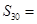 __________.
__________.
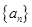 前
前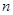 项和
项和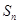 ,若
,若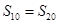 ,则
,则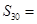 __________.
__________.0
试题分析:法一:设该等差数列首项、公差分别为
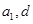 ,则由
,则由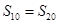 可得
可得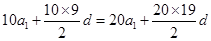 ,化简得
,化简得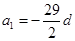 ,所以
,所以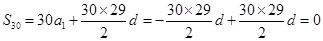 ;
;法二:由
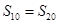 可得
可得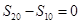 即
即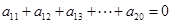 ,所以
,所以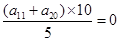 即
即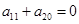 ,从而
,从而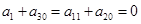 ,所以
,所以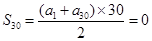 ;
;法三:因为数列
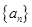 是等差数列,且
是等差数列,且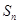 为其前
为其前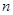 项和,所以
项和,所以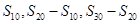 也成等差数列,所以
也成等差数列,所以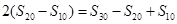 ,又因为
,又因为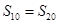 ,所以
,所以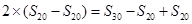 ,所以
,所以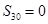 ;
;法四:由
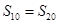 可知,该等差数列的公差不为0,而等差数列的前
可知,该等差数列的公差不为0,而等差数列的前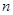 项和的形式为
项和的形式为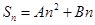 ,其中
,其中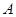 为公差的一半,由
为公差的一半,由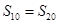 可知
可知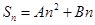 的对称轴为
的对称轴为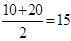 ,所以
,所以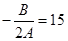 即
即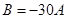 ,所以
,所以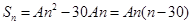 ,从而
,从而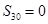 .
.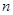 项和.
项和.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
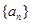 ,把
,把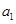 作为新数列
作为新数列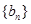 的第一项,把
的第一项,把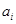 或
或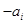 (
(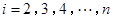 )作为新数列
)作为新数列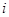 项,数列
项,数列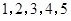 的一个生成数列是
的一个生成数列是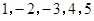 .已知数列
.已知数列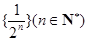 的生成数列,
的生成数列,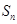 为数列
为数列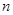 项和.
项和.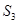 的所有可能值;
的所有可能值;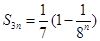 ,求数列
,求数列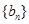 的通项公式;
的通项公式;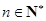 ,
,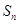 的所有可能值组成的集合为
的所有可能值组成的集合为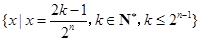 .
.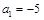 ,
,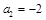 ,记
,记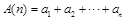 ,
,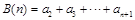 ,
,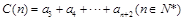 ,若对于任意
,若对于任意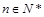 ,A(n),B(n),C(n)成等差数列.
,A(n),B(n),C(n)成等差数列.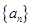 是公比为
是公比为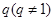 的等比数列,且
的等比数列,且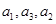 成等差数列.
成等差数列.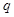 的值;
的值;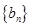 是以
是以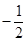 为首项,
为首项,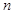 项和
项和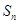 .
.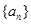 的前
的前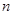 项和为
项和为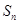 ,已知
,已知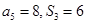 ,则
,则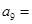 ( )
( )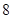 B.
B.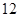 C.
C.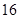 D 20
D 20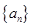 中,若
中,若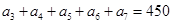 ,则
,则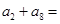 ( )
( )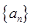 是等差数列,
是等差数列,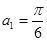 ,
,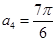 ,设
,设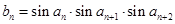 ,则数列
,则数列