题目内容
已知关于x的实系数一元二次方程ax2+bx+c=0有两个虚数根x1、x2,若|x1-x2|=2,且2+ai=c-1+i,求方程的根x1、x2.
解 由题可知,a、b、c是实数,又2+ai=c-1+i,∴ .
.
∵x1、x2是方程x2+bx+3=0的两个虚数根,|x1-x2|=2
∴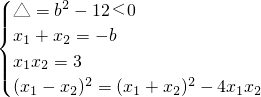 .
.
∴|x1-x2|2=|(x1-x2)2-4x1x2|,即|b2-12|=4,解得 .
.
当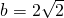 时,解
时,解 ,得
,得 ,
,
即方程的根为 .
.
当 时,解
时,解 ,得
,得 ,
,
即方程的根为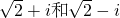 .
.
分析:根据2+ai=c-1+i,a,c是实数,可求出a,c的值,再根据韦达定理,求出x1+x1,x1x2,用含b的式子表示,再代入|x1-x2|=2中,即可求出b值,把a,b,c的值代入方程ax2+bx+c=0,利用求根公式就可求出x1、x2.
点评:本题主要考查一元二次方程的根的分布与系数的关系,考查分类讨论思想,转化思想,是中档题.
 .
.∵x1、x2是方程x2+bx+3=0的两个虚数根,|x1-x2|=2
∴
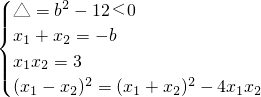 .
. ∴|x1-x2|2=|(x1-x2)2-4x1x2|,即|b2-12|=4,解得
 .
.当
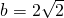 时,解
时,解 ,得
,得 ,
,即方程的根为
 .
. 当
 时,解
时,解 ,得
,得 ,
,即方程的根为
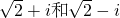 .
.分析:根据2+ai=c-1+i,a,c是实数,可求出a,c的值,再根据韦达定理,求出x1+x1,x1x2,用含b的式子表示,再代入|x1-x2|=2中,即可求出b值,把a,b,c的值代入方程ax2+bx+c=0,利用求根公式就可求出x1、x2.
点评:本题主要考查一元二次方程的根的分布与系数的关系,考查分类讨论思想,转化思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的一根在
的一根在 内,另一根在
内,另一根在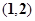 内,则点
内,则点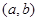 所在区域的面积为
所在区域的面积为 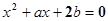 的一根在
的一根在 内,另一根在
内,另一根在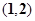 内,则点
内,则点 所在区域的面积为
所在区域的面积为