题目内容
(本小题满分12分)
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,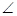 BCD=60
BCD=60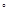 ,E是CD的中点,PA
,E是CD的中点,PA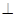 底面ABCD,PA=2.
底面ABCD,PA=2.
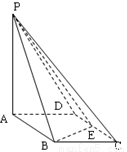
(1)证明:平面PBE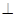 平面PAB;
平面PAB;
(2)求平面PAD和平面PBE所成二面角的正弦值。
【答案】
(1)根据面面垂直的判定定理来分析得到证明。主要是证明AH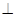 平面PBE
平面PBE
(2)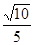
【解析】
试题分析:(1)略……………………………………………………………………5分
(2)延长AD,BE相交于F,联结PF,过A作AH⊥PB于H,
平面PBE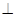 平面PAB知,AH
平面PAB知,AH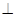 平面PBE,
平面PBE,
过H作HG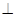 PF于联结AG,
PF于联结AG,

则∠AGH为所求锐二面角的平面角……………………………8分
计算略
sin∠AGH=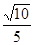 …………………………………………………12分
…………………………………………………12分
法2 向量法(略)
考点:本试题考查了面面垂直和线面角的求解。
点评:对于立体几何中面面垂直的证明,一般可以通过两种方法来得到。几何法,就是面面垂直的判定定理,或者运用向量法来得到,同理对于角的求解也是这样的两种方法,进而反而系得到结论。属于中档题。

练习册系列答案
相关题目