题目内容
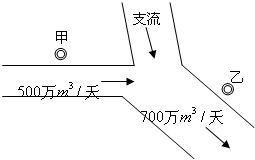 如图,在一条河流的上、下游分别有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.
如图,在一条河流的上、下游分别有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.(1)求河流在经过乙厂后污水含量的百分比约是多少?(精确到0.01%)
(2)根据环保要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两家工厂都必须各自处理一部分污水.已知甲厂处理污水的成本是1000元/万m3,乙厂处理污水的成本是1000元/万m3,求甲、乙两厂每天分别处理多少万m3污水,才能使两厂处理污水的总费用最少?最小总费用是多少元?
分析:(1)根据题意,写出甲厂排放的污水在流到乙厂时有多少被净化,从而得出河流在经过乙厂后污水的总含量,最后写出河流在经过乙厂后污水含量的百分比即可;
(2)先设设甲、乙两厂每天分别处理污x,,y万m3,两厂处理污水的总费用为z元,依题意得列出约束条件和目标函数,最后依据线性规则的方法求出目标函数的最大值即可.
(2)先设设甲、乙两厂每天分别处理污x,,y万m3,两厂处理污水的总费用为z元,依题意得列出约束条件和目标函数,最后依据线性规则的方法求出目标函数的最大值即可.
解答: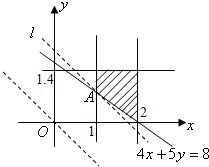 解:(1)由题意,甲厂排放的污水在流到乙厂时有2×20%=0.4(万m3)被净化,
解:(1)由题意,甲厂排放的污水在流到乙厂时有2×20%=0.4(万m3)被净化,
所以河流在经过乙厂后污水的总含量为(2-0.4)+1.4=3(万m3).
故河流在经过乙厂后污水含量的百分比约是
≈0.43%.(6分)
(2)设甲、乙两厂每天分别处理污x,y万m3,两厂处理污水的总费用为z元.z=1000×1+800×0.8=1640
即
目标函数为z=1000x+800y.9(8分)
作可行域,如图.(11分)
平移直线l:4x+5y=0,当直线经过点A(1,0.8)时,z取最小值,
此时(元)(13分)
故甲、乙两厂每天应分别处理1万m3、0.8万m3污水,才能使两厂处理污水的总费用最小,
且最小总费用是1640元.(15分)
 解:(1)由题意,甲厂排放的污水在流到乙厂时有2×20%=0.4(万m3)被净化,
解:(1)由题意,甲厂排放的污水在流到乙厂时有2×20%=0.4(万m3)被净化,所以河流在经过乙厂后污水的总含量为(2-0.4)+1.4=3(万m3).
故河流在经过乙厂后污水含量的百分比约是
| 3 |
| 700 |
(2)设甲、乙两厂每天分别处理污x,y万m3,两厂处理污水的总费用为z元.z=1000×1+800×0.8=1640
|
|
目标函数为z=1000x+800y.9(8分)
作可行域,如图.(11分)
平移直线l:4x+5y=0,当直线经过点A(1,0.8)时,z取最小值,
此时(元)(13分)
故甲、乙两厂每天应分别处理1万m3、0.8万m3污水,才能使两厂处理污水的总费用最小,
且最小总费用是1640元.(15分)
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
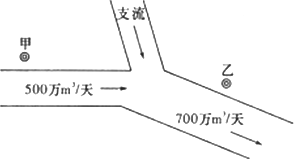
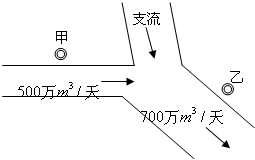 如图,在一条河流的上、下游分别有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.
如图,在一条河流的上、下游分别有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.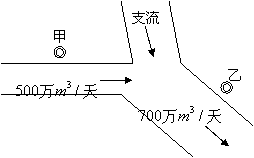 (2)根据环保要求,整个河流中污水含量不能超过
(2)根据环保要求,整个河流中污水含量不能超过