题目内容
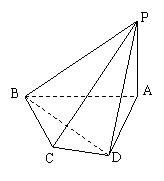
 如图,四棱锥A-BCDE中,侧面△ADE是等边三角形,在底面等腰梯形BCDE中,CD∥BE,DE=2,CD=4,∠CDE=60°,M为DE的中点,F为AC的中点,AC=4.
如图,四棱锥A-BCDE中,侧面△ADE是等边三角形,在底面等腰梯形BCDE中,CD∥BE,DE=2,CD=4,∠CDE=60°,M为DE的中点,F为AC的中点,AC=4.(I)求证:平面ADE⊥平面BCD;
(II)FB∥平面ADE.
分析:(I)由△ADE是边长为2的等边三角形,可求出AM,利用余弦定理解△DMC,可求出MC,进而由勾股定理可得AM⊥MC,进而结合线面垂直的判定定理和面面垂直的判定定理,可得平面ADE⊥平面BCD;
(II)取DC的中点N,连接FN,NB,由线面平行判定定理可分别证明出FN∥平面ADE和BN∥平面ADE,进而由面面平行的判定定理可得平面ADE∥平面FNB,再由面面平行的性质得到FB∥平面ADE.
(II)取DC的中点N,连接FN,NB,由线面平行判定定理可分别证明出FN∥平面ADE和BN∥平面ADE,进而由面面平行的判定定理可得平面ADE∥平面FNB,再由面面平行的性质得到FB∥平面ADE.
解答:证明:(Ⅰ)∵△ADE是等边三角形,DE=2,M是DE的中点,
∴AM⊥DE,AM=
.…(2分)
∵在△DMC中DM=1,∠CDM=60°,CD=4,…(3分)
∴MC2=42+12-2×4×1•cos60°=13,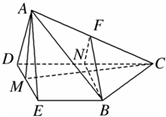
∴MC=
.
在△AMC中,AM2+MC2=(
)2+(
)2=42=AC2,…(4分)
∴△AMC是直角三角形.
∴AM⊥MC.
又∵AM⊥DE,MC∩DE=M,MC,DE?平面BCD
∴AM⊥平面BCD.
又∵AM?平面ADE,
∴平面ADE⊥平面BCD.…(6分)
(Ⅱ)取DC的中点N,连接FN,NB.
∵AC=DC,F,N点分别是AC,DC的中点,
∴FN∥AD.
又FN?平面ADE,AD?平面ADE,
∴FN∥平面ADE.…(8分)
∵点N是DC的中点,
∴BC=NC,
又∠BCN=60°,
∴△BCN是等边三角形,
∴BN∥DE.
又BN?平面ADE,ED?平面ADE,
∴BN∥平面ADE.
∵FN∩BN=N,
∴平面ADE∥平面FNB.
∵FB?平面FNB,
∴FB∥平面ADE.…(12分)
∴AM⊥DE,AM=
| 3 |
∵在△DMC中DM=1,∠CDM=60°,CD=4,…(3分)
∴MC2=42+12-2×4×1•cos60°=13,

∴MC=
| 13 |
在△AMC中,AM2+MC2=(
| 3 |
| 13 |
∴△AMC是直角三角形.
∴AM⊥MC.
又∵AM⊥DE,MC∩DE=M,MC,DE?平面BCD
∴AM⊥平面BCD.
又∵AM?平面ADE,
∴平面ADE⊥平面BCD.…(6分)
(Ⅱ)取DC的中点N,连接FN,NB.
∵AC=DC,F,N点分别是AC,DC的中点,
∴FN∥AD.
又FN?平面ADE,AD?平面ADE,
∴FN∥平面ADE.…(8分)
∵点N是DC的中点,
∴BC=NC,
又∠BCN=60°,
∴△BCN是等边三角形,
∴BN∥DE.
又BN?平面ADE,ED?平面ADE,
∴BN∥平面ADE.
∵FN∩BN=N,
∴平面ADE∥平面FNB.
∵FB?平面FNB,
∴FB∥平面ADE.…(12分)
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,熟练掌握空间线面关系的判定定理,性质及几何特征是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=
(2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=
 BC,AB=AC=
BC,AB=AC=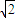 B.
B.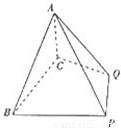
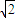 BC,AB=AC=
BC,AB=AC=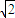 B.
B.