题目内容
已知数列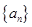 满足
满足 ,
, 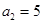 ,
,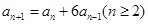 .
.
(1)求证: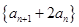 是等比数列;
是等比数列;
(2)求证: 是等比数列并求数列
是等比数列并求数列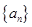 的通项公式;
的通项公式;
(3)设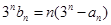 ,且
,且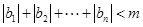 对于
对于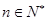 恒成立,求
恒成立,求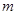 的取值范围.
的取值范围.
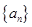 满足
满足 ,
, 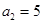 ,
,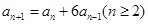 .
.(1)求证:
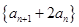 是等比数列;
是等比数列;(2)求证:
 是等比数列并求数列
是等比数列并求数列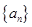 的通项公式;
的通项公式;(3)设
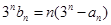 ,且
,且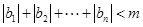 对于
对于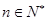 恒成立,求
恒成立,求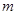 的取值范围.
的取值范围.(1)由an+1=an+6an-1,an+1+2an=3(an+2an-1) (n≥2),∵a1=5,a2=5,∴a2+2a1=15
故数列{an+1+2an}是以15为首项,3为公比的等比数列 …………5分
(2)由(1)得an+1+2an=5·3n ,∴ (an+1-3n+1)=-2(an-3n),
故数列 是以2为首项,-2为公比的等比数列,∴ an-3n=2(-2)n-1 ,
是以2为首项,-2为公比的等比数列,∴ an-3n=2(-2)n-1 ,
即an=3n+2(-2)n-1=3n-(-2)n ………9分
(3)由3nbn=n(3n-an)=n[3n-3n+(-2)n]=n(-2)n,∴bn=n(- )n
)n
令Sn=|b1|+|b2|+…+|bn|= +2(
+2( )2+3(
)2+3( )3+…+n(
)3+…+n( )n
)n
 Sn=(
Sn=( )2+2(
)2+2( )3+…+(n-1)(
)3+…+(n-1)(  )n+n(
)n+n( )n+1 …………11分
)n+1 …………11分
得 Sn=
Sn= +(
+( )2+(
)2+( )3+…+(
)3+…+( )n-n(
)n-n( )n+1=2[1-(
)n+1=2[1-( )n]-n(
)n]-n( )n+1
)n+1
∴ Sn=6[1-( )n]-3n(
)n]-3n( )n+1<6,要使得|b1|+|b2|+…+|bn|<m对于n∈N*恒成立,
)n+1<6,要使得|b1|+|b2|+…+|bn|<m对于n∈N*恒成立,
只须m≥6
故数列{an+1+2an}是以15为首项,3为公比的等比数列 …………5分
(2)由(1)得an+1+2an=5·3n ,∴ (an+1-3n+1)=-2(an-3n),
故数列
 是以2为首项,-2为公比的等比数列,∴ an-3n=2(-2)n-1 ,
是以2为首项,-2为公比的等比数列,∴ an-3n=2(-2)n-1 ,即an=3n+2(-2)n-1=3n-(-2)n ………9分
(3)由3nbn=n(3n-an)=n[3n-3n+(-2)n]=n(-2)n,∴bn=n(-
 )n
)n令Sn=|b1|+|b2|+…+|bn|=
 +2(
+2( )2+3(
)2+3( )3+…+n(
)3+…+n( )n
)n Sn=(
Sn=( )2+2(
)2+2( )3+…+(n-1)(
)3+…+(n-1)(  )n+n(
)n+n( )n+1 …………11分
)n+1 …………11分得
 Sn=
Sn= +(
+( )2+(
)2+( )3+…+(
)3+…+( )n-n(
)n-n( )n+1=2[1-(
)n+1=2[1-( )n]-n(
)n]-n( )n+1
)n+1∴ Sn=6[1-(
 )n]-3n(
)n]-3n( )n+1<6,要使得|b1|+|b2|+…+|bn|<m对于n∈N*恒成立,
)n+1<6,要使得|b1|+|b2|+…+|bn|<m对于n∈N*恒成立,只须m≥6
略

练习册系列答案
相关题目
 满足:
满足: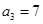 ,
,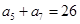 ,
, .
.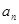 及
及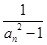 (
( ),求数列
),求数列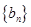 的前n项和
的前n项和 。
。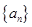 ,
, 且
且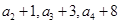 为等比数列
为等比数列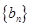 的前三项.
的前三项.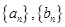 的通项公式;
的通项公式;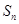 ,求
,求 .
.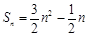 .数列{an}满足
.数列{an}满足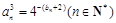 ,数列{cn}满足
,数列{cn}满足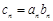 .
.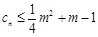 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.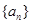 的前n项的和为
的前n项的和为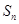 ,利用倒序求和的方法得:
,利用倒序求和的方法得: ;类似地,记等比数列
;类似地,记等比数列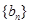 的前n项的积为
的前n项的积为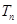 ,且
,且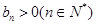 ,试类比等差数列求和的方法,将
,试类比等差数列求和的方法,将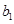 ,末项
,末项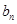 与项数n的一个关系式,即
与项数n的一个关系式,即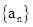 中,已知
中,已知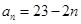 ,则前
,则前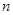 项和
项和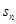 取最大值时所对应的项数
取最大值时所对应的项数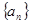 是公比大于1的等比数列,
是公比大于1的等比数列,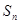 为数列
为数列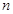 项和,已知
项和,已知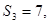 且
且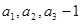 成等差数列。
成等差数列。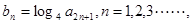 求和:
求和: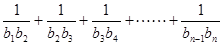 。
。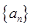 中,
中,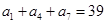 ,
,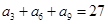 ,则数列
,则数列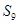 等于( )
等于( )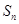 是等差数列
是等差数列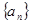 的前
的前 项和,若
项和,若
