题目内容
已知命题p:关于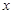 的不等式
的不等式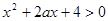 对一切
对一切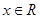 恒成立,命题q:函数
恒成立,命题q:函数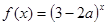 是增函数,若p或q为真,p且q为假,求实数
是增函数,若p或q为真,p且q为假,求实数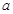 的取值范围.
的取值范围.
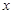 的不等式
的不等式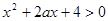 对一切
对一切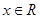 恒成立,命题q:函数
恒成立,命题q:函数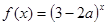 是增函数,若p或q为真,p且q为假,求实数
是增函数,若p或q为真,p且q为假,求实数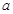 的取值范围.
的取值范围.解:设g(x)=x2+2ax+4,由于关于x的不等式x2+2ax+4>0对一切x∈R恒成立,所以函数g(x)的图象开口向上且与x轴没有交点,故Δ=4a2-16<0,∴-2<a<2.又∵函数f(x)=(3-2a)x是增函数,∴3-2a>1,∴a<1.
又由于p或q为真,p且q为假,可知p和q一真一假.
(1)若p真q假,则∴1≤a<2;
(2)若p假q真,则∴a≤-2.
综上可知,所求实数a的取值范围为1≤a<2,或a≤-2.
又由于p或q为真,p且q为假,可知p和q一真一假.
(1)若p真q假,则∴1≤a<2;
(2)若p假q真,则∴a≤-2.
综上可知,所求实数a的取值范围为1≤a<2,或a≤-2.
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
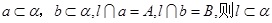
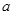 ∥
∥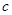 ,
,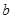 ∥
∥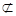
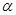 ,
,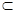
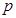 :
: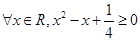 ,则命题
,则命题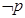 是 .
是 . p为真命题,求m的取值范围。
p为真命题,求m的取值范围。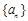 ,定义向量
,定义向量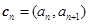 ,
,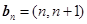 ,
,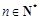 . 下列命题中真命题是 ( )
. 下列命题中真命题是 ( )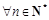 总有
总有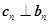 成立,则数列
成立,则数列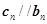 成立,则数列
成立,则数列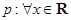 ,
,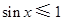 ,则( )
,则( )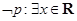 ,
,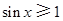
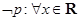 ,
,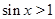
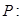 存在
存在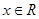 ,使得
,使得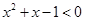 ,则
,则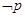 为 .
为 .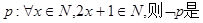 ( )
( )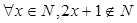
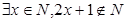
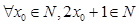
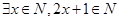
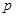 :
: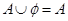 ,命题
,命题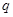 :
: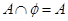 ,则下列说法正确的是
,则下列说法正确的是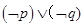 为假
为假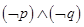 为真
为真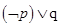 为假
为假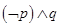 为真
为真