题目内容
设椭圆C∶![]() (a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点.
(a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点.

(1)求a的取值范围;
(2)(理)若椭圆上的点到焦点的最短距离为![]() ,求椭圆的方程;
,求椭圆的方程;
(文)如果椭圆的两个焦点与短轴的两个端点恰好是正方形的四个顶点,求椭圆的方程;
(3)(理)对(2)中的椭圆C,直线l∶y=kx+m(k≠0)与C交于不同的两点M、N,若线段MN的垂直平分线恒过点A(0,-1),求实数m的取值范围.
(文)过(2)中椭圆右焦点F2且不与坐标轴垂直的直线l交椭圆于M、N两点,线段MN的垂直平分线与x轴交于点Q,求点Q的横坐标的取值范围.
答案:
解析:
解析:
|
(1)由已知, ∴方程组 故 (2)(理)设椭圆上的点 则 ∵ 于是, ∴所求椭圆方程为 (直接给出 (2)(文)由已知可得 所以所求椭圆方程是 (3)(理)由 ∵直线 ①设 ∴ 又∵线段 即 ②由①,②得 ∴实数 (3)(文) 设 ∴线段 在上式中令 ∴ |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
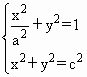 有实数解,从而
有实数解,从而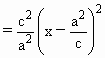 (
( ,解得
,解得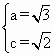 . 9分
. 9分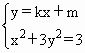 得
得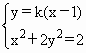 得,
得,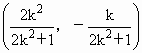 . 12分
. 12分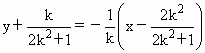 ,
,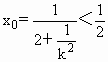 ,所以点
,所以点
 (“a>b〉0)的左焦点为
(“a>b〉0)的左焦点为 ,椭圆过点P(
,椭圆过点P( )
) 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.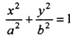 (a〉b>0)的左焦点为
(a〉b>0)的左焦点为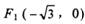 ,椭圆过点P(
,椭圆过点P(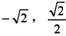 )
)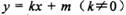 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
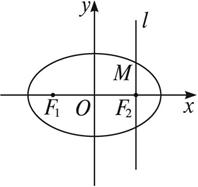
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围. (a>b>0)的左、右两个焦点分别为F1、F2.过右焦点F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(
(a>b>0)的左、右两个焦点分别为F1、F2.过右焦点F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(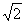 ,1).
,1).