题目内容
选修4-4:坐标系与参数方程(本小题满分10分)
已知极坐标的极点在平面直角坐标系的原点 处,极轴与
处,极轴与 轴的正半轴重合,且长度单位相同.直线
轴的正半轴重合,且长度单位相同.直线 的极坐标方程为:
的极坐标方程为: ,点
,点 ,参数
,参数 .
.
(Ⅰ)求点 轨迹的直角坐标方程;
轨迹的直角坐标方程;
(Ⅱ)求点 到直线
到直线 距离的最大值.
距离的最大值.
(Ⅰ)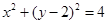 ;(II)
;(II)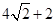 .
.
解析试题分析:(Ⅰ) 且参数
且参数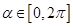 ,
,
所以点 的轨迹方程为
的轨迹方程为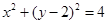 .··················· 3分
.··················· 3分
(Ⅱ)因为 ,所以
,所以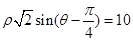 ,
,
所以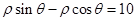 ,所以直线
,所以直线 的直角坐标方程为
的直角坐标方程为 .····· 6分
.····· 6分
法一:由(Ⅰ) 点 的轨迹方程为
的轨迹方程为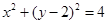 ,圆心为
,圆心为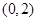 ,半径为2.
,半径为2.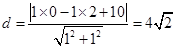 ,所以点
,所以点 到直线
到直线 距离的最大值
距离的最大值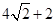 .····· 10分
.····· 10分
法二: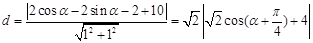 ,当
,当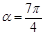 ,
,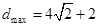 ,
,
即点 到直线
到直线 距离的最大值
距离的最大值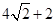 . 10分
. 10分
考点:极坐标方程与直角坐标方程的互化;点到直线的距离公式。
点评:一般情况下,我们要把参数方程或极坐标方程转化为直角坐标方程来做,属于基础题型。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10 cm,AP∶PB=1∶5,那么⊙O的半径是
A.5 cm cm | B.4 cm cm |
C.3 cm cm | D.2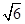 cm cm |
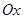 中,直线
中,直线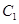 的极坐标方程为
的极坐标方程为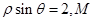 是
是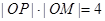 ,记点P的轨迹为
,记点P的轨迹为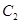 。
。 距离的最大值。
距离的最大值。 中,把矩阵
中,把矩阵 确定的压缩变换
确定的压缩变换 与矩阵
与矩阵 确定的旋转变换
确定的旋转变换 进行复合,得到复合变换
进行复合,得到复合变换 .
.
 在复合变换
在复合变换 的方程.
的方程. 的参数方程为
的参数方程为 (
(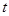 为参数),
为参数), 、
、 分别为直线
分别为直线 轴、
轴、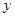 轴的交点,线段
轴的交点,线段 的中点为
的中点为 .
. 为极点,
为极点, 的极坐标方程.
的极坐标方程. 的解集与关于
的解集与关于 的解集相等.
的解集相等.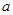 ,
, 的值;
的值; 的最大值,以及取得最大值时
的最大值,以及取得最大值时 .
.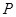 是圆
是圆 上一动点,点
上一动点,点 满足
满足 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程. 与直线
与直线 相切,求实数a的值。
相切,求实数a的值。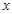 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线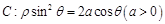 ,已知过点
,已知过点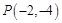 的直线
的直线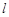 的参数方程为:
的参数方程为: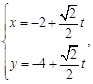 直线
直线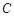 分别交于
分别交于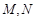
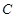 和直线
和直线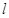 的普通方程;
的普通方程;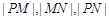 成等比数列,求
成等比数列,求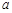 的值.
的值.  ,以极点为平面直角坐标系的原点,极轴为X轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为X轴的正半轴,建立平面直角坐标系,直线 的参数方程是:
的参数方程是: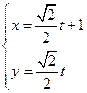 ,求直线
,求直线