题目内容
已知函数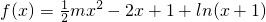
(Ⅰ)当m>0时,求函数的单调区间;
(Ⅱ)当m≥1时,曲线C:y=f(x)在点P(0,1)处的切线l与C有且只有一个公共点,
求m的取值的集合M.
解:由题设知: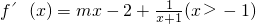
(Ⅰ)当m>0时,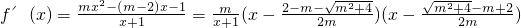 ,
,
而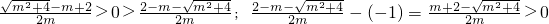
∴函数f(x)单调递增区间为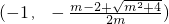 ∪
∪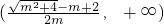 ;
;
单调递减区间为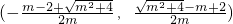 .
.
(Ⅱ)由题设知:P∈C,f'(0)=-1,切线l的方程为y=-x+1,
于是方程: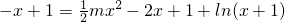 ,即
,即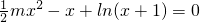 有且只有一个实数根;
有且只有一个实数根;
设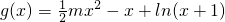 ,得g(0)=0;
,得g(0)=0;
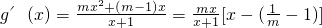 ,
,
当m=1时,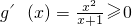 ,g(x)为增函数,符合题设;
,g(x)为增函数,符合题设;
当m>1时,有 ,得x∈(0,+∞),
,得x∈(0,+∞),
g'(x)>0,g(x)在此区间单调递增,g(x)>0;
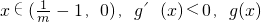 在此区间单调递减,g(x)>0;
在此区间单调递减,g(x)>0;
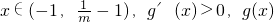 在此区间单调递增,
在此区间单调递增,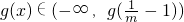 ;
;
此区间存在零点,即得m>1不符合题设;
∴由上述知:M={1}.
分析:根据函数f(x)的解析式求出f(x)的导函数,
(Ⅰ)把求出的导函数通分并分解因式后,由导函数的正负即可得到函数f(x)的单调区间;
(Ⅱ)由题意可知点P在曲线C上,把点P的横坐标代入导函数中求出的函数值即为切线方程的斜率,根据切点坐标和求出的斜率写出切线的方程,与曲线C的方程联立,消去y后得到关于x的一元二次方程只有一个解,设方程左边的式子等于g(x),且得到g(0)=0,求出g(x)的导函数,分m=1和m大于1两种情况考虑:当m=1时,代入得到g(x)的导函数大于等于0,即g(x)为增函数,符合题意;当m大于1时,根据导函数的正负讨论函数的单调性,进而得到函数在m大于1时有零点,不合题意,综上,得到满足题意m的取值范围.
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导函数的正负判断函数的单调性,是一道中档题.
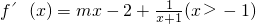
(Ⅰ)当m>0时,
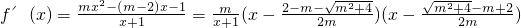 ,
,而
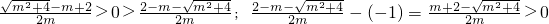
∴函数f(x)单调递增区间为
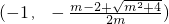 ∪
∪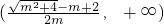 ;
;单调递减区间为
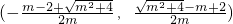 .
.(Ⅱ)由题设知:P∈C,f'(0)=-1,切线l的方程为y=-x+1,
于是方程:
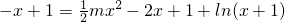 ,即
,即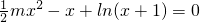 有且只有一个实数根;
有且只有一个实数根;设
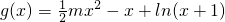 ,得g(0)=0;
,得g(0)=0;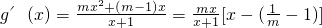 ,
,当m=1时,
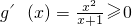 ,g(x)为增函数,符合题设;
,g(x)为增函数,符合题设;当m>1时,有
 ,得x∈(0,+∞),
,得x∈(0,+∞),g'(x)>0,g(x)在此区间单调递增,g(x)>0;
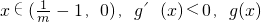 在此区间单调递减,g(x)>0;
在此区间单调递减,g(x)>0;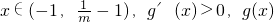 在此区间单调递增,
在此区间单调递增,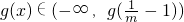 ;
;此区间存在零点,即得m>1不符合题设;
∴由上述知:M={1}.
分析:根据函数f(x)的解析式求出f(x)的导函数,
(Ⅰ)把求出的导函数通分并分解因式后,由导函数的正负即可得到函数f(x)的单调区间;
(Ⅱ)由题意可知点P在曲线C上,把点P的横坐标代入导函数中求出的函数值即为切线方程的斜率,根据切点坐标和求出的斜率写出切线的方程,与曲线C的方程联立,消去y后得到关于x的一元二次方程只有一个解,设方程左边的式子等于g(x),且得到g(0)=0,求出g(x)的导函数,分m=1和m大于1两种情况考虑:当m=1时,代入得到g(x)的导函数大于等于0,即g(x)为增函数,符合题意;当m大于1时,根据导函数的正负讨论函数的单调性,进而得到函数在m大于1时有零点,不合题意,综上,得到满足题意m的取值范围.
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导函数的正负判断函数的单调性,是一道中档题.

练习册系列答案
相关题目
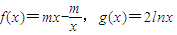 .
.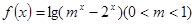
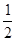 时,求f(x)的定义域
时,求f(x)的定义域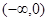 上的单调性并给出证明。
上的单调性并给出证明。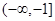 上恒取正值,求m的取值范围。
上恒取正值,求m的取值范围。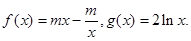
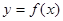 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;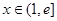 时,不等式
时,不等式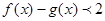 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
 存在两个零点,求m的取值范围;
存在两个零点,求m的取值范围; 。
。