题目内容
(本小题满分12分)已知函数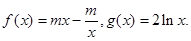
(1)当m=2时,求曲线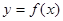 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;
(2)若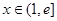 时,不等式
时,不等式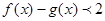 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】
.解:(1)m=2时,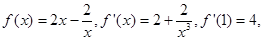 ……………………2分
……………………2分
切点坐标为(1,0),∴切线方程为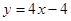 ……………………………………2分
……………………………………2分
(2)m=1时,令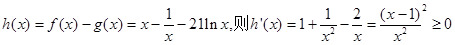
∴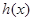 在(0,+∞)上是增函数.
……………………………………………………4分
在(0,+∞)上是增函数.
……………………………………………………4分
又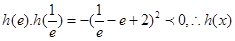 在
在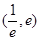 上有且只有一个零点……………5分
上有且只有一个零点……………5分
∴方程 有且仅有一个实数根;………………………………………………5分
有且仅有一个实数根;………………………………………………5分
(或说明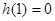 也可以)
也可以)
(3)由题意知,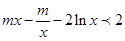 恒成立,即
恒成立,即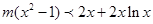 恒成立,`
恒成立,`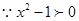
则当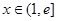 时,
时,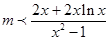 恒成立,……………………………………………………7分
恒成立,……………………………………………………7分
令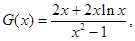 当
当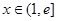 时,
时,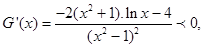 …………………9分
…………………9分
则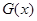 在
在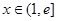 时递减,∴
时递减,∴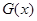 在
在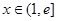 时的最小值为
时的最小值为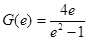 ,…11分
,…11分
则m的取值范围是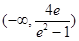 ……………………………………………………………………12分
……………………………………………………………………12分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目