题目内容
(满分12分)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.
已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
【答案】
(1)x=3或x=-1.(2)0<a<1
【解析】解:(1)当a=1,b=-2时,f(x)=x2-x-3=x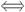 x2-2x-3=0
x2-2x-3=0
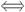 (x-3)(x+1)=0
(x-3)(x+1)=0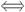 x=3或x=-1,
x=3或x=-1,
∴f(x)的不动点为x=3或x=-1.
(2)对于任意实数b,f(x)恒有两个相异不动点
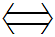 对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根
对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根
即ax2+bx+b-1=0恒有两个不等实根
 对任意实数b,Δ=b2-4a(b-1)>0恒成立
对任意实数b,Δ=b2-4a(b-1)>0恒成立
 对任意实数b,b2-4ab+4a>0恒成立
对任意实数b,b2-4ab+4a>0恒成立
 Δ′=16a2-16a<0
Δ′=16a2-16a<0
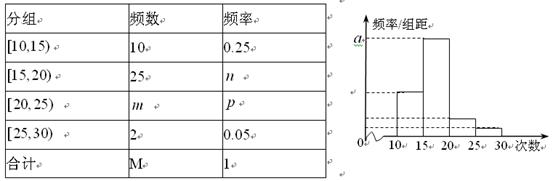
 a(a-1)<0
a(a-1)<0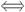 0<a<1.
0<a<1.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 及图中
及图中 的值;
的值;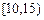 内的人数;
内的人数; 内的概率.
内的概率. 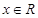 ,试比较
,试比较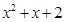 与
与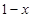 的大小;
的大小;
 的定义域为R,求实数k的取值范围。
的定义域为R,求实数k的取值范围。 
 是抛物线
是抛物线 上的点,过焦点F的直线FAn交抛物线另一点
上的点,过焦点F的直线FAn交抛物线另一点 。
。
 并
并 为抛物线上分别为
为抛物线上分别为 与
与 为切点的两条切线的交点,求证
为切点的两条切线的交点,求证
 ):
):