题目内容
(本小题两小题,每题6分,满分12分)
⑴对任意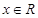 ,试比较
,试比较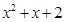 与
与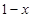 的大小;
的大小;
⑵已知函数 的定义域为R,求实数k的取值范围。
的定义域为R,求实数k的取值范围。
【答案】
⑴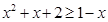 。 ⑵
。 ⑵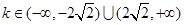
【解析】
试题分析:(1)根据作差法比较大小是一种重要的方法。同时要注意差式的变形技巧的运用。
(2)利用对数函数定义域为R,说明了无论x取什么样的数,表达式真数恒大于零,那么说明二次函数开口向上,判别式小于零得到。
⑴∵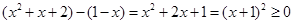 ,∴
,∴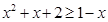 。
。
⑵∵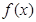 的定义域为
的定义域为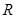 ,即
,即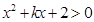 恒成立,∴
恒成立,∴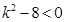 ,
,
即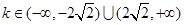
考点:本题主要考查配方法的运用,为判定差是大于零还是小于零,配方法也是常用的方法之一,比差法是比较两个代数式值的大小的常用方法,此题正是有效地利用了这两个方法,使问题得到解决,同时也考查了函数的定义域为R的理解和运用。
点评:解决该试题的关键是要比较两式的大小,可以运用比差法,把两个式子相减,可以得运用配方法来比较与零的大小关系,要使得对数函数定义域为R,说明了对数的真数部分恒大于零。

练习册系列答案
相关题目
 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余
 道题,乙答对每道题
道题,乙答对每道题 .
.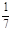 .现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,
.现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,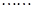 ,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求: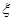 的数学期望(用分数表示,精确到0.01).
的数学期望(用分数表示,精确到0.01).