题目内容
例
( 2005全国卷III)已知函数![]() ,
,![]() (Ⅰ)求
(Ⅰ)求![]() 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设![]() ,函数
,函数![]() ,若对于任意
,若对于任意![]() ,总存在
,总存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范围。
的取值范围。
![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() 的值域为[-4,-3];
的值域为[-4,-3];![]()
解析:
解析(Ⅰ) 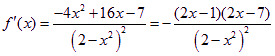 ,令
,令![]() 解得
解得![]() 或
或![]() ,在
,在![]() ,
,![]() 所以
所以![]() 为单调递减函数;在
为单调递减函数;在![]() ,
,![]() 所以
所以![]() 为单调递增函数;又
为单调递增函数;又![]() ,即
,即![]() 的值域为[-4,-3],所以
的值域为[-4,-3],所以![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() 的值域为[-4,-3].( 单调区间为闭区间也可以).
的值域为[-4,-3].( 单调区间为闭区间也可以).
(Ⅱ)∵![]() ,又
,又![]() ,当
,当![]() 时,
时,![]() ,
,
因此,当![]() 时,
时,![]() 为减函数,从而当
为减函数,从而当![]() 时,有
时,有![]() .
.
又![]() ,即当
,即当![]() 时,有
时,有![]() ,
,
任给![]() ,有
,有![]() ,存在
,存在![]() 使得
使得![]() ,
,
则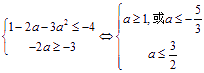 又
又![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() 。
。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
