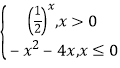题目内容
【题目】已知 ![]() ,
, ![]() ,函数
,函数 ![]() 的最小值为4.
的最小值为4.
(1)求 ![]() 的值;
的值;
(2)求 ![]() 的最小值.
的最小值.
【答案】
(1)解:因为, ![]() ,
,
所以 ![]() ,当且仅当
,当且仅当 ![]() 时,等号成立,又
时,等号成立,又 ![]() ,
, ![]() ,
,
所以 ![]() ,所以
,所以 ![]() 的最小值为
的最小值为 ![]() ,所以
,所以 ![]() .
.
(2)解:由(1)知 ![]() ,
, ![]() .
.![]()
当且仅当 ![]() ,
, ![]() 时,
时, ![]() 的最小值为
的最小值为 ![]() .
.
【解析】(1)根据绝对值的性质,可得| x + a | + | x b | ≥ | a b | = | a + b | ,所以 ![]() ,当且仅当
,当且仅当 ![]() 时,等号成立,又
时,等号成立,又 ![]() ,
, ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() 的最小值为
的最小值为 ![]() ,所以
,所以 ![]() .
.
(2)因为 a + b = 4 , b = 4 a ,将b参数化掉最后变成一个一元二次方程,就可以求出其最小值.
【考点精析】解答此题的关键在于理解复合函数单调性的判断方法的相关知识,掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”,以及对二次函数在闭区间上的最值的理解,了解当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目