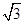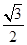题目内容
在△ABC中,a,b,c分别为内角A,B,C所对的边长,a=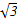 ,
,
b=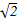 ,1+2cos(B+C)=0,求边BC上的高.
,1+2cos(B+C)=0,求边BC上的高.
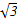 ,
,b=
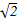 ,1+2cos(B+C)=0,求边BC上的高.
,1+2cos(B+C)=0,求边BC上的高.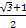
由1+2cos(B+C)=0和B+C=π-A,得
1-2cosA=0,cosA= ,sinA=
,sinA=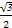 .
.
由正弦定理,得sinB=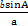 =
=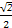 .
.
由b<a知B<A,所以B不是最大角,B<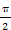 ,
,
从而cosB=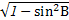 =
=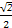 .
.
由上述结果知
sinC=sin(A+B)=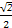 ×(
×(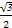 +
+ ).
).
设边BC上的高为h,则有h=bsinC=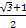 .
.
1-2cosA=0,cosA=
 ,sinA=
,sinA=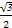 .
.由正弦定理,得sinB=
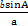 =
=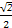 .
.由b<a知B<A,所以B不是最大角,B<
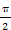 ,
,从而cosB=
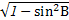 =
=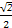 .
.由上述结果知
sinC=sin(A+B)=
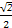 ×(
×(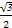 +
+ ).
).设边BC上的高为h,则有h=bsinC=
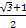 .
.
练习册系列答案
相关题目
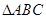 中,角
中,角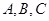 的对边分别为
的对边分别为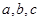 ,且
,且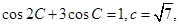 又
又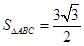 .
.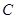 的大小;
的大小; 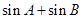 的值.
的值.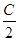 +ccos2
+ccos2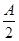 =
=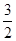 b.
b.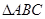 中,角
中,角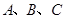 所对边分别为
所对边分别为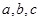 ,已知
,已知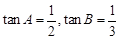 ,且最长边的边长为
,且最长边的边长为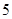 .求:
.求: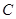 的正切值及其大小;
的正切值及其大小;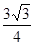 ,求a的值.
,求a的值.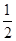 c+bcosC.
c+bcosC.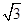 ,求b的最小值.
,求b的最小值. b,sin B=sin C,则B等于________.
b,sin B=sin C,则B等于________.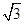 sin xcos x+2cos2x+m在区间
sin xcos x+2cos2x+m在区间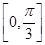 上的最大值为2.
上的最大值为2.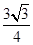 ,求边长a.
,求边长a.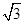 ,则S△ABC等于 ( ).
,则S△ABC等于 ( ).