题目内容
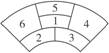
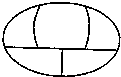
某城市在中心广场建造一个花圃，花圃分为6个部分（如图）．现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有 种．（以数字作答）
【答案】分析：由题意来看6部分种4种颜色的花，又从图形看知必有2组同颜色的花，从同颜色的花入手分类求．②与⑤同色，则③⑥也同色或④⑥也同色，③与⑤同色，则②④或⑥④同色，②与④且③与⑥同色，根据分类计数原理得到结果．
解答：解：从题意来看6部分种4种颜色的花，
又从图形看知必有2组同颜色的花，从同颜色的花入手分类求．
（1）②与⑤同色，则③⑥也同色或④⑥也同色，
所以共有N1=4×3×2×2×1=48种；
（2）③与⑤同色，则②④或⑥④同色，
所以共有N2=4×3×2×2×1=48种；
（3）②与④且③与⑥同色，则共有N3=4×3×2×1=24种．
∴共有N=N1+N2+N3=48+48+24=120种．
故答案为：120
点评：这是一道理科的高考题，本题还可以这样解：记颜色为A，B，C，D四色，先安排1，2，3有A43种不同的栽法，
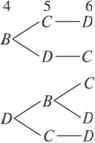
不妨设1，2，3已分别栽种A，B，C，则4，5，6栽种方法共5种，
由以下树状图清晰可见．
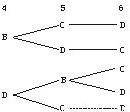
根据分步计数原理，不同栽种方法有N=A43×5=120．
解答：解：从题意来看6部分种4种颜色的花，
又从图形看知必有2组同颜色的花，从同颜色的花入手分类求．
（1）②与⑤同色，则③⑥也同色或④⑥也同色，
所以共有N1=4×3×2×2×1=48种；
（2）③与⑤同色，则②④或⑥④同色，
所以共有N2=4×3×2×2×1=48种；
（3）②与④且③与⑥同色，则共有N3=4×3×2×1=24种．
∴共有N=N1+N2+N3=48+48+24=120种．
故答案为：120
点评：这是一道理科的高考题，本题还可以这样解：记颜色为A，B，C，D四色，先安排1，2，3有A43种不同的栽法，
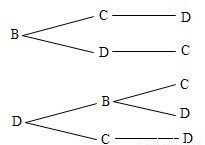
不妨设1，2，3已分别栽种A，B，C，则4，5，6栽种方法共5种，
由以下树状图清晰可见．
根据分步计数原理，不同栽种方法有N=A43×5=120．
练习册系列答案
相关题目
15、某城市在中心广场建造一个花圃，花圃分为6个部分（如图）．现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有
某城市在中心广场建造一个花圃（如图），花圃分为5个部分，现要将4种颜色的花全部种在花圃中，每部分种一种颜色，且相邻部分的花不同色，则不同的栽种方法共有
