题目内容
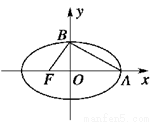
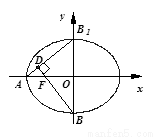
 如图所示,椭圆中心在原点,F是左焦点,直线AB1与BF交于D,且∠BDB1=90°,则椭圆的离心率为( )
如图所示,椭圆中心在原点,F是左焦点,直线AB1与BF交于D,且∠BDB1=90°,则椭圆的离心率为( )分析:确定直线AB1的斜率、直线BF的斜率,可得斜率的积为-1,由此可求椭圆的离心率.
解答:解:设左顶点A(-a,0),左焦点F(-c,0),上顶点B1(0,b),下顶点B(0,-b)
则直线AB1的斜率为
,直线BF的斜率为-
因为∠BDB1=90°,直线AB1与直线BF交于D,所以AB1⊥BF
所以
•(-
)=-1
所以b2=ac
又因为a2=b2+c2,所以a2=ac+c2,
所以e2+e-1=0
所以e=
因为0<e<1,所以e=
故选B.
则直线AB1的斜率为
| b |
| a |
| b |
| c |
因为∠BDB1=90°,直线AB1与直线BF交于D,所以AB1⊥BF
所以
| b |
| a |
| b |
| c |
所以b2=ac
又因为a2=b2+c2,所以a2=ac+c2,
所以e2+e-1=0
所以e=
-1±
| ||
| 2 |
因为0<e<1,所以e=
| ||
| 2 |
故选B.
点评:本题考查椭圆的性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
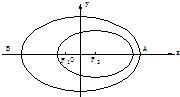 2003年10月15日9时,“神舟”五号载人飞船发射升空,于9时9分50秒准确进入预定轨道,开始巡天飞行.该轨道是以地球的中心F2为一个焦点的椭圆.选取坐标系如图所示,椭圆中心在原点.近地点A距地面200km,远地点B距地面350km.已知地球半径R=6371km.
2003年10月15日9时,“神舟”五号载人飞船发射升空,于9时9分50秒准确进入预定轨道,开始巡天飞行.该轨道是以地球的中心F2为一个焦点的椭圆.选取坐标系如图所示,椭圆中心在原点.近地点A距地面200km,远地点B距地面350km.已知地球半径R=6371km.
 与BF交于D,
与BF交于D,  ,则椭圆的离心率为( )
,则椭圆的离心率为( )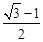 B.
B.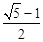 C.
C.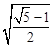 D.
D.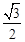
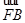 ⊥
⊥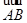 时,其离心率为
时,其离心率为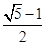 ,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于( )
,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于( )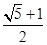 B.
B. 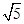 -1 D.
-1 D.