题目内容
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 | 2004 | 2006 | 2008 | 2010 | 2012 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量与年份之间的回归直线方程
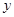 =
= x+
x+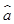
(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.
(1)  (2)
(2)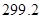 万吨
万吨
解析试题分析:
(1)根据题中的表格,可知年份从 ,所以可以简化表格,将年份都减去2008,然后可直接求出
,所以可以简化表格,将年份都减去2008,然后可直接求出 求出线性回归方程.
求出线性回归方程.
(2)根据(1)直接将2014代入即可.
试题解析:
(1)由所给数据可以看出,年需求量与年份之间是近似直线上升,下面来求回归直线方程.为此对数据预处理如下:年份-2008 -4 -2 0 2 4 需求量-257 -21 -11 0 19 29
对预处理后的数据,容易算得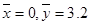 ,
, ,
,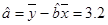
由上述计算结果,知所求回归直线方程为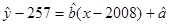 ,即
,即 ①
①
(2)利用直线方程①,可预测2014年的粮食需求量为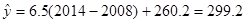 (万吨).
(万吨).
考点 线性回归方程.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
某网站体育版块足球栏目组发起了“射手的连续进球与射手在场上的区域位置有关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| | 有关系 | 无关系 | 不知道 |
| 40岁以下 | 800 | 450 | 200 |
| 40岁以上(含40岁) | 100 | 150 | 300 |
(2)在持“不知道”态度的人中,用分层抽样的方法抽取10人看作一个总体.①从这10人中选取3人,求至少一人在40岁以下的概率;②从这10人中人选取3人,若设40岁以下的人数为X,求X的分布列和数学期望.
某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.
| 组别 | 分组 | 回答正确的人数 | 回答正确的人数占本组的概率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | 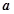 | 0.9 |
| 第3组 | [35,45) | 27 |  |
| 第4组 | [45,55) | 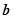 | 0.36 |
| 第5组 | [55,65) | 3 |  |
(1)分别求出
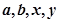 的值;
的值;(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图:
男生
女生
(1)根据以上两个直方图完成下面的2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | | | |
| 女生 | | | |
| 总计 | | | |
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
(注:
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K2=
 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)(3)若从成绩在[130,140]的学生中任取2人,求取到的2人中至少有1名女生的概率.
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
 名工人年龄数据如下表:
名工人年龄数据如下表: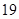


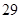
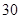
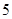
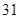

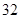

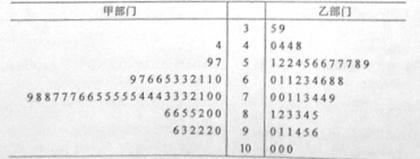


 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在 之间的概率;
之间的概率; 小镇当某件讯息发布后,
小镇当某件讯息发布后, 小时之内听到该讯息的人口是全镇人
小时之内听到该讯息的人口是全镇人 口的
口的 ﹪,其中
﹪,其中 是某个大于0的常数,今有某讯息,假设在发布后3小时之内已经
是某个大于0的常数,今有某讯息,假设在发布后3小时之内已经 有70﹪的人口听到该讯息。又设最快要
有70﹪的人口听到该讯息。又设最快要 小时后,有99﹪的人口已听到该讯息,则
小时后,有99﹪的人口已听到该讯息,则 小时。(保留一位小数)
小时。(保留一位小数)