题目内容
已知二次函数f(x)的二次项系数为a,且不等式f(x)<-2x的解集为(1,3).(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;(2)若f(x)的最小值为负数,求a的取值范围.
解析:本题综合考查一元二次方程、一元二次不等式和二次函数的关系及其性质,重点是互相之间的转化.在(1)中,通过不等式f(x)<-2x的解集为(1,3),用二次函数的标根式把不等式转化成函数,再根据韦达定理将问题转化成关于a的方程.在(2)中,既可以根据二次函数的最值公式将题意转化成不等式,也可以用配方法求最值.
答案:(1)∵f(x)+2x<0的解集为(1,3),∴设f(x)+2x=a(x-1)(x-3),则a>0.因而
f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a①
由方程f(x)+6a=0,得ax2-(2+4a)x+9a=0②?
∵方程②有两个相等的根,
∴Δ=[-(2+4a)]2-4a·9a=0,?
即5a2-4a-1=0.解得a=1或a=-![]() .
.
由于a>0,舍去a=-![]() .将a=1代入①得f(x)的解析式f(x)=x2-6x+3.?
.将a=1代入①得f(x)的解析式f(x)=x2-6x+3.?
(2)由f(x)=ax2-2(1+2a)x+3a
=a(x-![]() )2-
)2-![]() 及a>0,可得f(x)的最小值为-
及a>0,可得f(x)的最小值为-![]() .?
.?
由题意可得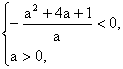 解得a>0.
解得a>0.
故当f(x)的最小值为负数时,实数a的取值范围是a>0.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目